题目内容
5．若函数f（x）=x2+bx+c的图象的顶点在第四象限，则函数f′（x）的图象是（ ）| A． |  | B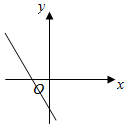． |  | C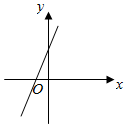． |  | D． |  |
分析 先根据二次函数的判断出a，b的符号，再求导，根据一次函数的性质判断所经过的象限即可．
解答 解：∵函数f（x）=ax2+bx+c的图象开口向上且顶点在第四象限，
∴a＞0，-$\frac{b}{2a}$＞0，
∴b＜0，
∵f′（x）=2ax+b，
∴函数f′（x）的图象经过一，三，四象限，
∴A符合，
故选A．
点评 本题考查了导数的运算和一次函数，二次函数的图象和性质，属于基础题．
练习册系列答案
相关题目
13．设△ABC的内角A、B、C所对的边长分别为a、b、c，且acosB=3，bsinA=4．若△ABC的面积S=10，则△ABC的周长为（ ）
| A． | 10 | B． | $10+2\sqrt{3}$ | C． | $10+2\sqrt{5}$ | D． | 12 |
10．已知函数f（x）=ln$\frac{x}{2}$+$\frac{1}{2}$，g（x）=ex-2，对于?m∈R，?n∈（0，+∞）使得f（m）=g（n）成立，则n-m的最大值为（ ）
| A． | -ln2 | B． | ln2 | C． | 2$\sqrt{e}$-3 | D． | e2-3 |
9．阅读程序框图（如图），如果输出的函数值在[1，3]上，则输入的实数x取值范围是（ ）
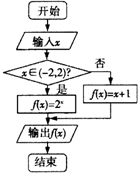
| A． | [0，log23] | B． | [-2，2] | C． | [0，log23]∪{2} | D． | [-2，log23]∪{2} |