题目内容
12. 某高三年级从甲(文)乙(理)两个年级组各选出7名学生参加高校自主招生数学选拔考试,他们取得的成绩(满分:100分)的茎叶图如图所示,其中甲组学生的平均分是85分,乙组学生成绩的中位数是83分.
某高三年级从甲(文)乙(理)两个年级组各选出7名学生参加高校自主招生数学选拔考试,他们取得的成绩(满分:100分)的茎叶图如图所示,其中甲组学生的平均分是85分,乙组学生成绩的中位数是83分.(1)求x和y的值;
(2)从成绩在90分以上的学生中随机取两名学生,求甲组至少有一名学生的概率.
分析 (1)利用茎叶图,和平均数的定义即可得到x的值,根据中位数的定义即可求出y的值,
(2)从这五名学生任意抽取两名学生共有10种情况,其中甲组至少有一名学生共有7种情况,根据概率公式计算即可.
解答 解(1)∵甲组学生的平均分是85,
∴$\frac{92+96+80+80+x+85+79+78}{7}=85$.∴x=5.…(2分)
∵乙组学生成绩的中位数是83,∴y=3.…(4分)
(2)甲组成绩在90(分)以上的学生有两名,分别记为A,B,
乙组成绩在90(分)以上的学生有三名,分别记为C,D,E.…(6分)
从这五名学生任意抽取两名学生共有10种情况:
(A,B),(A,C),(A,D),(A,E),(B,C),(B,D),(B,E),(C,D),(C,E),(D,E) …(8分)
其中甲组至少有一名学生共有7种情况:
(A,B),(A,C),(A,D),(A,E),(B,C),(B,D),(B,E)
记“从成绩在90(分)以上的学生中随机抽取两名学生,甲组至少有一名学生”为事件M,
则$P(M)=\frac{7}{10}$.…(12分)
点评 本小题主要考查茎叶图、样本均值、样本中位数、概率等知识,考查或然与必然的数学思想方法,以及数据处理能力、运算求解能力和应用意识.

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
4.中心为原点,一个焦点为$F(0,5\sqrt{2})$的椭圆截直线y=3x-2所得的弦的中点的横坐标为$\frac{1}{2}$,则椭圆的方程为( )
| A. | $\frac{x^2}{25}+\frac{y^2}{75}=1$ | B. | $\frac{x^2}{75}+\frac{y^2}{25}=1$ | C. | $\frac{{2{x^2}}}{75}+\frac{{2{y^2}}}{25}=1$ | D. | $\frac{{2{x^2}}}{25}+\frac{{2{y^2}}}{75}=1$ |
1.已知命题p:?x∈(0,$\frac{π}{2}$),使得cosx≥x,则该命题的否定是( )
| A. | ?x∈(0,$\frac{π}{2}$),使得cos x>x | B. | ?x∈(0,$\frac{π}{2}$),使得cos x≥x | ||
| C. | ?x∈(0,$\frac{π}{2}$),使得cos x<x | D. | ?x∈(0,$\frac{π}{2}$),使得cos x<x |
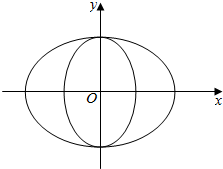 如图,曲线Γ由两个椭圆T1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$和椭圆T2:$\frac{y^2}{b^2}+\frac{x^2}{c^2}=1({b>c>0})$组成,当a,b,c成等比数列时,称曲线Γ为“猫眼曲线”.
如图,曲线Γ由两个椭圆T1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$和椭圆T2:$\frac{y^2}{b^2}+\frac{x^2}{c^2}=1({b>c>0})$组成,当a,b,c成等比数列时,称曲线Γ为“猫眼曲线”.