题目内容
17.已知函数$f(x)=2sin(2x+\frac{π}{4})-1$,求(1)f(x)最小正周期及单调增区间.
(2)满足不等式f(x)≥0的x取值范围的集合.
分析 (1)由条件利用正弦函数的周期性、单调性,得出结论.
(2)由不等式可得sin(2x+$\frac{π}{4}$)≥$\frac{1}{2}$,故有2kπ+$\frac{π}{6}$≤2x+$\frac{π}{4}$≤2kπ+$\frac{5π}{6}$,由此求得x取值范围的集合.
解答 解:(1)由函数$f(x)=2sin(2x+\frac{π}{4})-1$,可得它的最小正周期为$\frac{2π}{2}$=π,
令2kπ-$\frac{π}{2}$≤2x+$\frac{π}{4}$≤2kπ+$\frac{π}{2}$,求得 kπ-$\frac{3π}{8}$≤x≤kπ+$\frac{π}{8}$,
可得函数的增区间为[kπ-$\frac{3π}{8}$,kπ+$\frac{π}{8}$],k∈Z.
(2)不等式f(x)≥0,即 sin(2x+$\frac{π}{4}$)≥$\frac{1}{2}$,∴2kπ+$\frac{π}{6}$≤2x+$\frac{π}{4}$≤2kπ+$\frac{5π}{6}$,
求得kπ-$\frac{π}{24}$≤x≤kπ+$\frac{7π}{24}$,故不等式的解集为 {x|kπ-$\frac{π}{24}$≤x≤kπ+$\frac{7π}{24}$,k∈Z}.
点评 本题主要考查正弦函数的周期性、单调性,三角不等式的解法,属于基础题.

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
 某高三年级从甲(文)乙(理)两个年级组各选出7名学生参加高校自主招生数学选拔考试,他们取得的成绩(满分:100分)的茎叶图如图所示,其中甲组学生的平均分是85分,乙组学生成绩的中位数是83分.
某高三年级从甲(文)乙(理)两个年级组各选出7名学生参加高校自主招生数学选拔考试,他们取得的成绩(满分:100分)的茎叶图如图所示,其中甲组学生的平均分是85分,乙组学生成绩的中位数是83分.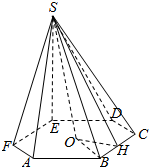 正六棱锥的底面周长为24,斜高SH与高SO所成的角为30°.
正六棱锥的底面周长为24,斜高SH与高SO所成的角为30°.