题目内容
 如图,在△ABC中,D、E分别是AC、BC的中点,M是DE的中点,若
如图,在△ABC中,D、E分别是AC、BC的中点,M是DE的中点,若| AB |
| a |
| BC |
| b |
(1)用
| a |
| b |
| AM |
(2)若N为线段AB的中点,求证:C、M、N三点共线.
考点:平面向量的基本定理及其意义,向量的三角形法则
专题:平面向量及应用
分析:利用向量的几何意义,表示出
,利用向量共线的充要条件得到两向量共线,进一步得出三点共线.
| AM |
解答:
解:(1)∵D、E分别是AC、BC的中点,M是DE的中点,
∴
=
-
=
-(
-
)=
-(
-
)=
+
=
(
+
)+
=
+
=
+
,
(2)∵
=
-
=
-
-
=-
-
,
=
-
=
-(
+
)=
+
-(
-
)=-
-
,
∴
=
又
与
有交点,
∴C、M、N三点共线.
∴
| AM |
| AC |
| MC |
| AC |
| DC |
| DM |
| AC |
| 1 |
| 2 |
| AC |
| 1 |
| 2 |
| DE |
| 1 |
| 2 |
| AC |
| 1 |
| 4 |
| AB |
| 1 |
| 2 |
| AB |
| BC |
| 1 |
| 4 |
| AB |
| 3 |
| 4 |
| AB |
| 1 |
| 2 |
| BC |
| 3 |
| 4 |
| a |
| 1 |
| 2 |
| b |
(2)∵
| MN |
| AN |
| AM |
| 1 |
| 2 |
| AB |
| 3 |
| 4 |
| a |
| 1 |
| 2 |
| b |
| 1 |
| 4 |
| a |
| 1 |
| 2 |
| b |
| MC |
| AM |
| AC |
| AM |
| AB |
| BC |
| 3 |
| 4 |
| a |
| 1 |
| 2 |
| b |
| a |
| b |
| 1 |
| 4 |
| a |
| 1 |
| 2 |
| b |
∴
| MN |
| MC |
又
| MN |
| MC |
∴C、M、N三点共线.
点评:本题考查向量的运算法则、向量共线的充要条件、利用向量共线解决三点共线,属于中档题

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
如图,△ABC内接于⊙O于A,AD切⊙O于A,∠BAD=60°,则∠ACB=( )


| A、120° | B、150° |
| C、90° | D、100° |
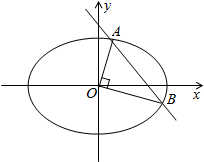 已知焦点在x轴上的椭圆
已知焦点在x轴上的椭圆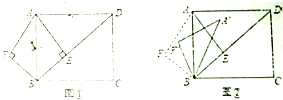 已知:如图①,在矩形ABCD中,AB=5,AD=
已知:如图①,在矩形ABCD中,AB=5,AD=