题目内容
已知函数f(x)=alnx-ax-3(a∈R).
(1)若a=-1,求函数f(x)的单调区间;
(2)若函数y=f(x)的图象在点(2,f(2))处的切线的倾斜角为45°,对于任意的t∈[1,2],函数g(x)=x3+x2[f′(x)+
]在区间(t,3)上总不是单调函数,求m的取值范围;
(3)若x1、x2∈[1,+∞),试比较ln(x1x2)与x1+x2-2的大小.
(1)若a=-1,求函数f(x)的单调区间;
(2)若函数y=f(x)的图象在点(2,f(2))处的切线的倾斜角为45°,对于任意的t∈[1,2],函数g(x)=x3+x2[f′(x)+
| m |
| 2 |
(3)若x1、x2∈[1,+∞),试比较ln(x1x2)与x1+x2-2的大小.
考点:利用导数研究函数的单调性,利用导数研究曲线上某点切线方程
专题:计算题,函数的性质及应用,导数的综合应用
分析:(1)代入a=-1求函数f(x)=-lnx+x-3的定义域,从而求导f′(x)=
;由导数确定函数的单调性;
(2)可知f′(2)=-
=tan45°;从而化简f(x)=-2lnx+2x-3,从而得 g(x)=x3+(2+
)x2-2x,求导g′(x)=3x2+(m+4)x-2;从而转化为零点的存在性问题;
(3)由(1)知f(x)=-lnx+x-3在(1,+∞)上单调递增,从而可得-lnx+x-1≥0,即lnx≤x-1;从而判断大小.
| x-1 |
| x |
(2)可知f′(2)=-
| a |
| 2 |
| m |
| 2 |
(3)由(1)知f(x)=-lnx+x-3在(1,+∞)上单调递增,从而可得-lnx+x-1≥0,即lnx≤x-1;从而判断大小.
解答:
解:(1)f(x)=-lnx+x-3的定义域为(0,+∞),
f′(x)=
;
则当x∈(1,+∞)时,f′(x)>0,当x∈(0,1)时,f′(x)<0;
故f(x)的单调增区间为[1,+∞),减区间为(0,1];
(2)由题意知,f′(2)=-
=tan45°;
故a=-2,
则f(x)=-2lnx+2x-3,
∴g(x)=x3+(2+
)x2-2x,
∴g′(x)=3x2+(m+4)x-2;
∵g(x)在区间(t,3)上总不是单调函数,且g′(0)=-2;
∴
;
由题意知:对于任意的t∈[1,2],g′(t)<0恒成立,
所以有:
,
∴-
<m<-9;
(3)由(1)知f(x)=-lnx+x-3在(1,+∞)上单调递增,
∴当x∈[1,+∞)时,f(x)≥f(1),即-lnx+x-1≥0,
故lnx≤x-1;
∵x1、x2∈[1,+∞),
∴ln(x1x2)=lnx1+lnx2≤x1+x2-2;
即ln(x1x2)≤x1+x2-2.
f′(x)=
| x-1 |
| x |
则当x∈(1,+∞)时,f′(x)>0,当x∈(0,1)时,f′(x)<0;
故f(x)的单调增区间为[1,+∞),减区间为(0,1];
(2)由题意知,f′(2)=-
| a |
| 2 |
故a=-2,
则f(x)=-2lnx+2x-3,
∴g(x)=x3+(2+
| m |
| 2 |
∴g′(x)=3x2+(m+4)x-2;
∵g(x)在区间(t,3)上总不是单调函数,且g′(0)=-2;
∴
|
由题意知:对于任意的t∈[1,2],g′(t)<0恒成立,
所以有:
|
∴-
| 37 |
| 3 |
(3)由(1)知f(x)=-lnx+x-3在(1,+∞)上单调递增,
∴当x∈[1,+∞)时,f(x)≥f(1),即-lnx+x-1≥0,
故lnx≤x-1;
∵x1、x2∈[1,+∞),
∴ln(x1x2)=lnx1+lnx2≤x1+x2-2;
即ln(x1x2)≤x1+x2-2.
点评:本题考查了导数的综合应用及存在性问题的应用,同时考查了函数的性质的判断与应用,属于中档题.

练习册系列答案
相关题目
已知全集U={1,2,3,4,5},集合A={1,3},B={3,4,5},则集合∁U(A∩B)=( )
| A、{3} |
| B、{4,5} |
| C、{1,2,4,5} |
| D、{2} |
运行如图所示的程序框图,则输出的结果S为( )


| A、2014 | B、2013 |
| C、1008 | D、1007 |
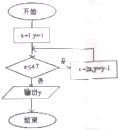
如图所示,程序框图(算法流程图)的输出结果是( )

| A、0 | B、-1 | C、-2 | D、-3 |
下列命题错误的是( )
| A、已知直线a∥b,且b∥c,则a∥c |
| B、已知直线a∥平面α,且直线b∥平面α,则a∥b |
| C、已知直线a∥平面α,过平面α内一点作b∥a,则b?α |
| D、过平面外一点可以做无数条直线与这个平面平行,并且这些直线都在同一平面内 |
 如图,在△ABC中,D、E分别是AC、BC的中点,M是DE的中点,若
如图,在△ABC中,D、E分别是AC、BC的中点,M是DE的中点,若