题目内容
已知a+b+c=0,abc=2,求证:a,b,c中至少有一个不小于2.
考点:反证法与放缩法
专题:证明题,不等式的解法及应用
分析:由于a+b+c=0,则a,b,c至少有一个为正数,不妨设c>0,则a+b=-c,ab=
,将a,b看作是x2+cx+
=0的两根,再由判别式大于等于0,即可得证.
| 2 |
| c |
| 2 |
| c |
解答:
证明:由于a+b+c=0,
则a,b,c至少有一个为正数,
不妨设c>0,则a+b=-c,
ab=
,
将a,b看作是x2+cx+
=0的两根,
则判别式△=c2-
≥0,
即有c≥2.
则a,b,c中至少有一个不小于2.
则a,b,c至少有一个为正数,
不妨设c>0,则a+b=-c,
ab=
| 2 |
| c |
将a,b看作是x2+cx+
| 2 |
| c |
则判别式△=c2-
| 8 |
| c |
即有c≥2.
则a,b,c中至少有一个不小于2.
点评:本题考查不等式的证明,考查判别式法证明不等式的方法,属于中档题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
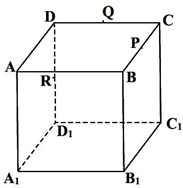 如图,正方体ABCD-A1B1C1D1的棱长为2,P,Q,R分别是棱BC,CD,DD1的中点.下列命题:
如图,正方体ABCD-A1B1C1D1的棱长为2,P,Q,R分别是棱BC,CD,DD1的中点.下列命题: 如图,a,b是异面直线,画出平面α,使a?α,且b∥α,并说明理由.
如图,a,b是异面直线,画出平面α,使a?α,且b∥α,并说明理由.