题目内容
6.已知tan(x+$\frac{π}{4}$)=3,则sinxcosx的值是$\frac{2}{5}$.分析 利用正切的和差公式展开,求解出tanx的值,根据同角三角函数关系式和万能公式化简后代入求值即可.
解答 解:由tan(x+$\frac{π}{4}$)=3,可得:$\frac{tanx+1}{1-tanx}=3$,
解得:tanx=$\frac{1}{2}$.
那么:sinxcosx=$\frac{sinxcosx}{si{n}^{2}x+co{s}^{2}x}$=$\frac{tanx}{ta{n}^{2}x+1}=\frac{\frac{1}{2}}{\frac{1}{4}+1}=\frac{2}{5}$.
故答案为$\frac{2}{5}$.
点评 本题主要考察了同角三角函数关系式和万能公式的应用,属于基本知识的考查.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.若函数f(x)为区间D上的凸函数,则对于D上的任意n个值x1、x2、…、xn,总有f(x1)+f(x2)+…+f(xn)≤nf($\frac{{x}_{1}+{x}_{2}+…+{x}_{n}}{n}$),现已知函数f(x)=sinx在[0,$\frac{π}{2}$]上是凸函数,则在锐角△ABC中,sinA+sinB+sinC的最大值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{3\sqrt{3}}{2}$ |
1.已知曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的渐近线方程为y=±$\frac{\sqrt{2}}{2}$x,则该曲线的离心率为( )
| A. | $\frac{\sqrt{6}}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\sqrt{3}$ |
18.若(1+2x)(1-2x)7=a0+a1x+a2x2+…+a8x8,则a0+a1+a2+…+a7的值为( )
| A. | -2 | B. | -3 | C. | 253 | D. | 126 |
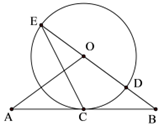 如图,直线AB经过⊙O上一点C,且OA=OB,CA=CB,⊙O交直线OB于E、D.
如图,直线AB经过⊙O上一点C,且OA=OB,CA=CB,⊙O交直线OB于E、D.