题目内容
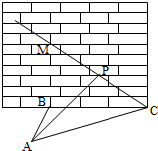如图，某人在垂直于水平地面ABC的墙面前的点A处进行射击训练，已知点A到墙面的距离为AB，某目标点P沿墙面上的射线CM移动，此人为了准确瞄准目标点P，需计算由点A观察点P的仰角θ的大小（仰角θ为直线AP与平面ABC所成的角）．若AB=15m，AC=25m，∠BCM=30°，则tanθ的最大值是（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点：正弦定理,解三角形的实际应用
专题：三角函数的求值,解三角形
分析：在直角三角形ABC中，由AB与AC的长，利用勾股定理求出BC的长，过P作PP′⊥BC，交BC于点P′，连接AP′，利用锐角三角函数定义表示出tanθ=
，设BP′=m，则CP′=20-m，利用锐角三角函数定义表示出PP′，利用勾股定理表示出AP′，表示出tanθ，即可确定出tanθ的值．
| PP′ |
| AP′ |
解答：
解：∵AB=15cm，AC=25cm，∠ABC=90°，
∴BC=20cm，
过P作PP′⊥BC，交BC于P′，连接AP′，则tanθ=
，
设BP′=x，则CP′=20-x，
由∠BCM=30°，得PP′=CP′tan30°=
（20-x），
在直角△ABP′中，AP′=
，
∴tanθ=
•
，
令y=
，则函数在x∈[0，20]单调递减，
∴x=0时，取得最大值为
=
，
若P′在CB的延长线上，PP′=CP′tan30°=
（20+x），
在直角△ABP′中，AP′=
，
∴tanθ=
•
，
令y=
，则y′=0可得x=
时，函数取得最大值
，
则tanθ的最大值是
．
解：∵AB=15cm，AC=25cm，∠ABC=90°，∴BC=20cm，
过P作PP′⊥BC，交BC于P′，连接AP′，则tanθ=
| PP′ |
| AP′ |
设BP′=x，则CP′=20-x，
由∠BCM=30°，得PP′=CP′tan30°=
| ||
| 3 |
在直角△ABP′中，AP′=
| 225+x2 |
∴tanθ=
| ||
| 3 |
| 20-x | ||
|
令y=
| 20-x | ||
|
∴x=0时，取得最大值为
20
| ||
| 45 |
4
| ||
| 9 |
若P′在CB的延长线上，PP′=CP′tan30°=
| ||
| 3 |
在直角△ABP′中，AP′=
| 225+x2 |
∴tanθ=
| ||
| 3 |
| 20+x | ||
|
令y=
| (20+x)2 |
| 225+x2 |
| 45 |
| 4 |
5
| ||
| 9 |
则tanθ的最大值是
5
| ||
| 9 |
点评：此题考查了正弦定理，锐角三角函数定义，以及解三角形的实际应用，弄清题意是解本题的关键．
练习册系列答案
相关题目
| 1+3i |
| 1-i |
| A、1+2i | B、-1+2i |
| C、1-2i | D、-1-2i |
等差数列{an}的公差为2，若a2，a4，a8成等比数列，则{an}的前n项和Sn=（ ）
| A、n（n+1） | ||
| B、n（n-1） | ||
C、
| ||
D、
|
乒乓球台面被网分成甲、乙两部分，如图，甲上有两个不相交的区域A，B，乙被划分为两个不相交的区域C，D，某次测试要求队员接到落点在甲上的来球后向乙回球，规定：回球一次，落点在C上记3分，在D上记1分，其它情况记0分．对落点在A上的来球，小明回球的落点在C上的概率为