题目内容
平面上一机器人在行进中始终保持与点F(1,0)的距离和到直线x=-1的距离相等,若机器人接触不到过点P(-1,0)且斜率为k的直线,则k的取值范围是 .
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:由抛物线的定义,求出机器人的轨迹方程,过点P(-1,0)且斜率为k的直线方程为y=k(x+1),代入y2=4x,利用判别式,即可求出k的取值范围.
解答:
解:由抛物线的定义可知,机器人的轨迹方程为y2=4x,
过点P(-1,0)且斜率为k的直线方程为y=k(x+1),
代入y2=4x,可得k2x2+(2k2-4)x+k2=0,
∵机器人接触不到过点P(-1,0)且斜率为k的直线,
∴△=(2k2-4)2-4k4<0,
∴k<-1或k>1.
故答案为:k<-1或k>1.
过点P(-1,0)且斜率为k的直线方程为y=k(x+1),
代入y2=4x,可得k2x2+(2k2-4)x+k2=0,
∵机器人接触不到过点P(-1,0)且斜率为k的直线,
∴△=(2k2-4)2-4k4<0,
∴k<-1或k>1.
故答案为:k<-1或k>1.
点评:本题考查抛物线的定义,考查直线与抛物线的位置关系,属于中档题.

练习册系列答案
相关题目
根据如图框图,对大于2的正数N,输出的数列的通项公式是( )


| A、an=2n |
| B、an=2(n-1) |
| C、an=2n |
| D、an=2n-1 |
已知b>0,log5b=a,lgb=c,5d=10,则下列等式一定成立的是( )
| A、d=ac | B、a=cd |
| C、c=ad | D、d=a+c |
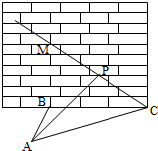 如图,某人在垂直于水平地面ABC的墙面前的点A处进行射击训练,已知点A到墙面的距离为AB,某目标点P沿墙面上的射线CM移动,此人为了准确瞄准目标点P,需计算由点A观察点P的仰角θ的大小(仰角θ为直线AP与平面ABC所成的角).若AB=15m,AC=25m,∠BCM=30°,则tanθ的最大值是( )
如图,某人在垂直于水平地面ABC的墙面前的点A处进行射击训练,已知点A到墙面的距离为AB,某目标点P沿墙面上的射线CM移动,此人为了准确瞄准目标点P,需计算由点A观察点P的仰角θ的大小(仰角θ为直线AP与平面ABC所成的角).若AB=15m,AC=25m,∠BCM=30°,则tanθ的最大值是( )