题目内容
(1)求证:当a、b、c为正数时,(a+b+c)(
+
+
)≥9.
(2)已知x>0,y>0,证明不等式:(x2+y2)
>(x3+y3)
.
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
(2)已知x>0,y>0,证明不等式:(x2+y2)
| 1 |
| 2 |
| 1 |
| 3 |
考点:不等式的证明
专题:证明题
分析:(1)将所证不等式的左端展开,重新组合,利用基本不等式即可证得结论成立;
(2)利用分析法,要证原不等式成立,只需证明变形后的不等式x2+y2>
xy成立即可,利用基本不等式,上式易证,从而证得原不等式成立.
(2)利用分析法,要证原不等式成立,只需证明变形后的不等式x2+y2>
| 2 |
| 3 |
解答:
(1)证明:左边=3+(
+
)+(
+
)+(
+
)≥3+2+2+2=9,
∴(a+b+c)(
+
+
)≥9…(6分)
(2)证明:(分析法)要证不等式:(x2+y2)
>(x3+y3)
,
只需证明(x2+y2)3>(x3+y3)2,
即:x6+y6+3x2y2(x2+y2)>x6+y6+2x3y3,
即:3x2y2(x2+y2)>2x3y3,
只需证:x2+y2>
xy,
∵x2+y2≥2xy>
xy成立,
∴(x2+y2)
>(x3+y3)
. …(12分)
| a |
| b |
| b |
| a |
| c |
| b |
| b |
| c |
| a |
| c |
| c |
| a |
∴(a+b+c)(
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
(2)证明:(分析法)要证不等式:(x2+y2)
| 1 |
| 2 |
| 1 |
| 3 |
只需证明(x2+y2)3>(x3+y3)2,
即:x6+y6+3x2y2(x2+y2)>x6+y6+2x3y3,
即:3x2y2(x2+y2)>2x3y3,
只需证:x2+y2>
| 2 |
| 3 |
∵x2+y2≥2xy>
| 2 |
| 3 |
∴(x2+y2)
| 1 |
| 2 |
| 1 |
| 3 |
点评:本题考查不等式的证明,着重考查基本不等式的应用,考查分析法、综合法,考查推理证明能力,属于中档题.

练习册系列答案
相关题目
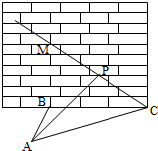 如图,某人在垂直于水平地面ABC的墙面前的点A处进行射击训练,已知点A到墙面的距离为AB,某目标点P沿墙面上的射线CM移动,此人为了准确瞄准目标点P,需计算由点A观察点P的仰角θ的大小(仰角θ为直线AP与平面ABC所成的角).若AB=15m,AC=25m,∠BCM=30°,则tanθ的最大值是( )
如图,某人在垂直于水平地面ABC的墙面前的点A处进行射击训练,已知点A到墙面的距离为AB,某目标点P沿墙面上的射线CM移动,此人为了准确瞄准目标点P,需计算由点A观察点P的仰角θ的大小(仰角θ为直线AP与平面ABC所成的角).若AB=15m,AC=25m,∠BCM=30°,则tanθ的最大值是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设函数f1(x)=x2,f2(x)=2(x-x2),f3(x)=
|sin2πx|,ai=
,i=0,1,2,…,99.记Ik=|fk(a1)-fk(a0)|+|fk(a2)-fk(a1)丨+…+|fk(a99)-fk(a98)|,k=1,2,3,则( )
| 1 |
| 3 |
| i |
| 99 |
| A、I1<I2<I3 |
| B、I2<I1<I3 |
| C、I1<I3<I2 |
| D、I3<I2<I1 |