题目内容
如果角α、β满足α+β=π,那么下列式子中正确的个数是( )
①sinα=sinβ; ②sinα=-sinβ;
③cosα=cosβ; ④cosα=-cosβ.
①sinα=sinβ; ②sinα=-sinβ;
③cosα=cosβ; ④cosα=-cosβ.
| A、1 | B、2 | C、3 | D、4 |
考点:运用诱导公式化简求值
专题:三角函数的求值
分析:利用诱导公式,对①②③④四个选项判断即可.
解答:
解:∵α+β=π,
∴sinα=sinβ,cosα=-cosβ,
∴①sinα=sinβ; ②sinα=-sinβ;③cosα=cosβ; ④cosα=-cosβ四个命题中正确的有两个,为①④;
故选:B.
∴sinα=sinβ,cosα=-cosβ,
∴①sinα=sinβ; ②sinα=-sinβ;③cosα=cosβ; ④cosα=-cosβ四个命题中正确的有两个,为①④;
故选:B.
点评:本题考查运用诱导公式化简求值,属于基础题.

练习册系列答案
相关题目
已知x>0,y>0,2x+y+2xy=8,则2x+y的最小值是( )
| A、3 | ||
| B、4 | ||
C、
| ||
D、
|
函数f(x)=-
x3+x2+3x的单调递增区间为( )
| 1 |
| 3 |
| A、(-3,1) |
| B、(-1,3) |
| C、(-∞,-1)和(3,+∞) |
| D、(-∞,-3)和(1,+∞) |
已知集合A={-1,0,1},B={x|x=|a+1|,a∈A},则A∩B=( )
| A、{0} | B、{1} |
| C、{0,1} | D、{0,1,2} |
不等式组
表示的平面区域为( )
|
| A、四边形及内部 |
| B、等腰三角形及内部 |
| C、在第一象限内的一个无界区域 |
| D、不含第一象限内的点的一个有界区域 |
一个员工需在一周内值班两天,其中恰有一天是星期六的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
若ax2+bx+c<0的解集为{x|x<-2或x>4},则对于函数f(x)=ax2+bx+c应有( )
| A、f(5)<f(2)<f(-1) |
| B、f(5)<f(-1)<f(2) |
| C、f(-1)<f(2)<f(5) |
| D、f(2)<f(-1)<f(5) |
如图,在正方体ABCD-A1B1C1D1中,异面直线DB1与BC1的所成角为( )
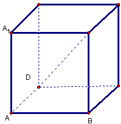

| A、60° | B、30° |
| C、90° | D、45° |