题目内容
已知f1(x)＝sin x＋cos x，记f2(x)＝f1′(x)，f3(x)＝f2′(x)，…，fn(x)＝fn－1′(x)(n∈N*，n≥2)，则
＝________.
0解析：f2(x)＝f1′(x)＝cos x－sin x，
f3(x)＝(cos x－sin x)′＝－sin x－cos x，
f4(x)＝－cos x＋sin x，f5(x)＝sin x＋cos x，
以此类推，可得出fn(x)＝fn＋4(x)，
又∵f1(x)＋f2(x)＋f3(x)＋f4(x)＝0，
练习册系列答案
黄冈经典趣味课堂系列答案
启东小题作业本系列答案
相关题目
已知函数y＝f(x)的图像是连续不间断的曲线，且有如下的对应值：
| x | 1 | 2 | 3 | 4 | 5 | 6 |
| y | 124.4 | 35 | －74 | 14.5 | －56.7 | －123.6 |
则函数y＝f(x)在区间[1,6]上的零点至少有( )
A．2个 B．3个
C．4个 D．5个
与y2＝x3－x2＋2x在x＝x0处切线的斜率的乘积为3，则x0的值为( )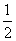
D．1
，其导函数记为f′(x)，则f(2 012)＋f′(2 012)＋f(－2 012)－f′(－2 012)＝________.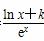
(k为常数，e是自然对数的底数)，曲线y＝f(x)在点(1，f(1))处的切线与x轴平行．
的最小正周期为π.
，求f(x)的单调递增区间．