题目内容
函数f(x)=x3-3x-1,若对于区间[-3,2]上的任意x1,x2,都有|f(x1)-f(x2)|≤t,则实数t的最小值是( )
A.20 B.18
C.3 D.0
A 因为f′(x)=3x2-3=3(x-1)(x+1),令f′(x)=0,得x=±1,所以-1,1为函数的极值点.又f(-3)=-19,f(-1)=1,
f(1)=-3,f(2)=1,所以在区间[-3,2]上f(x)max=1,f(x)min=-19.又由题设知在区间[-3,2]上f(x)max-f(x)min≤t,从而t≥20,所以t的最小值是20.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目

 x D.2x-2
x D.2x-2 =________.
=________. B.-
B.-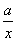 .
. ,则sin α=( )
,则sin α=( ) B.
B. D.
D. =________.
=________. B.
B.  C.
C.  D.
D. 
