题目内容
求函数y=
的定义域和值域．
| 2x |
| 1+2x |
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：根据指数函数的性质即可得到结论．
解答：
解：∵1+2x＞1，∴函数的定义域为R，
y=
=
=1-
，
∵1+2x＞1，∴0＜
＜1，-1＜-
＜0，0＜1-
＜1，
即0＜y＜1，
则函数的值域为（0，1）．
y=
| 2x |
| 1+2x |
| 2x+1-1 |
| 2x+1 |
| 1 |
| 1+2x |
∵1+2x＞1，∴0＜
| 1 |
| 1+2x |
| 1 |
| 1+2x |
| 1 |
| 1+2x |
即0＜y＜1，
则函数的值域为（0，1）．
点评：本题主要考查函数定义域和值域的求解，根据指数函数的性质是解决本题的关键．
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
在四棱锥P-ABCD中，AB∥DC，AB⊥平面PAD，PD=AD，AB=2DC，E是PB的中点．求证：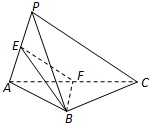
如图，在三棱锥P-ABC中，PA⊥PC，AB=PB，E，F分别是PA，AC的中点．求证：（1）EF∥平面PBC；