题目内容
下列命题中:
①不等式x+
≥2恒成立;
②在三角形ABC中,如果有sinA=sinB成立,则必有A=B;
③将两个变量所对应的点在平面直角坐标系中描出来,如果所描的点在散点图中没有显示任何关系则称变量间是不相关的;
④等差数列{an}的首项a1=-50,公差d=2,前n项和为Sn,则n=25或n=26是使Sn取到最大值;
其中为正确命题的序号是: .
①不等式x+
| 1 |
| x |
②在三角形ABC中,如果有sinA=sinB成立,则必有A=B;
③将两个变量所对应的点在平面直角坐标系中描出来,如果所描的点在散点图中没有显示任何关系则称变量间是不相关的;
④等差数列{an}的首项a1=-50,公差d=2,前n项和为Sn,则n=25或n=26是使Sn取到最大值;
其中为正确命题的序号是:
考点:命题的真假判断与应用
专题:简易逻辑
分析:①当x<0时,不等式x+
≥2不成立;
②在三角形ABC中,如果有sinA=sinB成立,则sinA=sinB?2cos
sin
=0,(*),又A,B∈(0,π),可知:(*)?A=B;
③将两个变量所对应的点在平面直角坐标系中描出来,如果所描的点在散点图中没有显示任何关系则称变量间是不相关的,正确;
④等差数列{an}的首项a1=-50,公差d=2,前n项和为Sn,可得Sn=-50n+
×2=(n-
)2-
,利用二次函数的单调性即可判断出.
| 1 |
| x |
②在三角形ABC中,如果有sinA=sinB成立,则sinA=sinB?2cos
| A+B |
| 2 |
| A-B |
| 2 |
③将两个变量所对应的点在平面直角坐标系中描出来,如果所描的点在散点图中没有显示任何关系则称变量间是不相关的,正确;
④等差数列{an}的首项a1=-50,公差d=2,前n项和为Sn,可得Sn=-50n+
| n(n-1) |
| 2 |
| 51 |
| 2 |
| 2601 |
| 4 |
解答:
解:①当x<0时,不等式x+
≥2不成立,因此不正确;
②在三角形ABC中,如果有sinA=sinB成立,则sinA=sinB?2cos
sin
=0,(*),又A,B∈(0,π),∴(*)?A=B,因此②正确;
③将两个变量所对应的点在平面直角坐标系中描出来,如果所描的点在散点图中没有显示任何关系则称变量间是不相关的,正确;
④等差数列{an}的首项a1=-50,公差d=2,前n项和为Sn,则Sn=-50n+
×2=(n-
)2-
,因此当n=25或n=26是使Sn取到最小值,因此不正确.
综上可得:只有②③正确.
故答案为:②③.
| 1 |
| x |
②在三角形ABC中,如果有sinA=sinB成立,则sinA=sinB?2cos
| A+B |
| 2 |
| A-B |
| 2 |
③将两个变量所对应的点在平面直角坐标系中描出来,如果所描的点在散点图中没有显示任何关系则称变量间是不相关的,正确;
④等差数列{an}的首项a1=-50,公差d=2,前n项和为Sn,则Sn=-50n+
| n(n-1) |
| 2 |
| 51 |
| 2 |
| 2601 |
| 4 |
综上可得:只有②③正确.
故答案为:②③.
点评:本题综合考查了基本不等式的性质、三角函数恒等变换、线性相关、等差数列的前n项和公式、二次函数的单调性等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
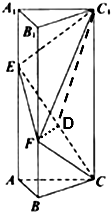 如图,已知正三棱柱ABC-A1B1C1的底面边长为2,侧棱长为3
如图,已知正三棱柱ABC-A1B1C1的底面边长为2,侧棱长为3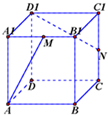 如图,正方体ABCD-A1B1C1D1中,M、N分别为A1B1、CC1的中点,求异面直线AM和D1N所成角
如图,正方体ABCD-A1B1C1D1中,M、N分别为A1B1、CC1的中点,求异面直线AM和D1N所成角