题目内容
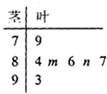 在某校举行的“校园艺术节”比赛上,七位评委为1号选手打出的分数的茎叶图如图所示,去掉一个最高分和一个最低分后,所剩数据的平均数为85,则m2+n2的最小值是
在某校举行的“校园艺术节”比赛上,七位评委为1号选手打出的分数的茎叶图如图所示,去掉一个最高分和一个最低分后,所剩数据的平均数为85,则m2+n2的最小值是考点:茎叶图
专题:概率与统计
分析:利用茎叶图由已知条件求出m+n=8,且m>0,n>0,由此能求出m2+n2的最小值是32.
解答:
解:由题意知:
(84+80+m+86+n+80+87)=85,
∴m+n=8,且m>0,n>0,
∴m2+n2+2mn=64,
∵mn≤(
)2=16,
∴m2+n2≥64-2×16=32.
当且仅当m=n=4时,取等号,
∴m2+n2的最小值是32.
故答案为:32.
| 1 |
| 5 |
∴m+n=8,且m>0,n>0,
∴m2+n2+2mn=64,
∵mn≤(
| n+m |
| 2 |
∴m2+n2≥64-2×16=32.
当且仅当m=n=4时,取等号,
∴m2+n2的最小值是32.
故答案为:32.
点评:本题考查两数的平方和的最小值的求法,是基础题,解题时要注意茎叶图和均值定理的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知x、y满足条件
,若目标函数z=ax+y取得最大值时的最优解有无数个,则实数a的值为( )
|
A、-
| ||
B、-
| ||
C、
| ||
D、
|
若a∈R,则复数z=
对应的点不可能在复平面的( )
| a+i |
| 1+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
函数y=x2(x≤0)的反函数是( )
A、y=
| ||
B、y=
| ||
C、y=-
| ||
D、y=-
|
 关于图中的正方体ABCD-A1B1C1D1,下列说法正确的有:
关于图中的正方体ABCD-A1B1C1D1,下列说法正确的有: