题目内容
若数列{an}的前n项的和Sn=3n-2,那么这个数列的通项公式为( )
A、an=(
| |||||||
B、an=an=3×(
| |||||||
| C、an=3n-2 | |||||||
D、an=
|
考点:数列递推式
专题:等差数列与等比数列
分析:当n=1时直接由Sn=3n-2求a1,当n≥2时,由an=Sn-Sn-1求通项公式,验证首项后得答案.
解答:
解:由Sn=3n-2,得a1=S1=31-2=1;
当n≥2时,an=Sn-Sn-1=3n-2-(3n-1-2)=2×3n-1.
当n=1时,上式不成立.
∴an=
.
故选:D.
当n≥2时,an=Sn-Sn-1=3n-2-(3n-1-2)=2×3n-1.
当n=1时,上式不成立.
∴an=
|
故选:D.
点评:本题考查了数列递推式,考查了由数列的前n项和求数列的通项公式,是中档题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
若方程
-
=1表示双曲线,则k的取值范围是( )
| x2 |
| k |
| y2 |
| k-2 |
| A、k>2 | B、k<0 |
| C、k>2,或k<0 | D、0<k<2 |
用“二分法”求方程x3-2x-1=0的一个近似解时,现在已经将一根锁定在在区间(1,2)内,则下一步可断定该根所在的区间为( )
| A、(1,1.4) |
| B、(1.4,2) |
| C、(1,1.5) |
| D、(1.5,2) |
如图所示的程序框图中输出的a的结果为( )


| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
 如图所示,在边长为
如图所示,在边长为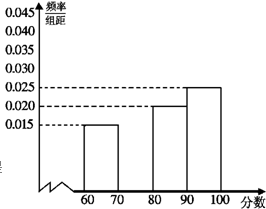 某集团公司对所属的200家企业进行年终考评,并依据考评得分(最低60分,最高100分,可以是小数)将其分别评定为A、B、C、D四个等级,标准如下表:
某集团公司对所属的200家企业进行年终考评,并依据考评得分(最低60分,最高100分,可以是小数)将其分别评定为A、B、C、D四个等级,标准如下表: