题目内容
9.已知椭圆$\frac{x^2}{36}+\frac{y^2}{49}=1$上的一点P到椭圆的一个焦点的距离为3,则P点到另一个焦点的距离( )| A. | 3 | B. | 4 | C. | 9 | D. | 11 |
分析 根据题意,由椭圆的标准方程可得a=7,进而由椭圆的定义可得P点到另一个焦点的距离为2a-3,计算可得答案.
解答 解:根据题意,椭圆的标准方程为$\frac{x^2}{36}+\frac{y^2}{49}=1$,
则其焦点在y轴上,且a=7,
又由改椭圆上上的一点P到椭圆的一个焦点的距离为3,
则P点到另一个焦点的距离为2a-3=2×7-3=11;
故选:D.
点评 本题考查椭圆的简单几何性质,注意要认真分析椭圆的标准方程,明确参数a.

练习册系列答案
相关题目
19.将函数f(x)=xsinx,当${x_1},{x_2}∈[-\frac{π}{2},\frac{π}{2}]$时,f(x1)>f(x2)成立,下列结论正确的是( )
| A. | x1>x2 | B. | x1>|x2| | C. | x1<x2 | D. | x${\;}_{1}^{2}$>x${\;}_{2}^{2}$ |
4.$tanϕ=-\sqrt{3}$,ϕ为第四象限角,则cosϕ=( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | -$\frac{{\sqrt{3}}}{2}$ |
18.已知函数f(x)=ax2+2ax+4(-3<a<0),其图象上两点的横坐标为x1、x&2满足x1<x2,且x1+x2=1+a,则由( )
| A. | f(x1)<f(x2) | B. | f(x1)=f(x2) | ||
| C. | f(x1)>f(x2) | D. | f(x1)、f(x&2)的大小不确定 |
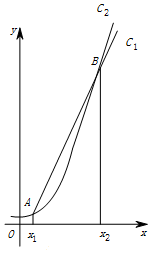 函数f(x)=2x和g(x)=x3的图象的示意图如图所示,设两函数的图象交于点A(x1,y1),B(x2,y2),且x1<x2.若x1∈[a,a+1],x2∈[b,b+1],且a,b∈{1,2,3,4,5,6,7,8,9,10,11,12},则a+b=10.
函数f(x)=2x和g(x)=x3的图象的示意图如图所示,设两函数的图象交于点A(x1,y1),B(x2,y2),且x1<x2.若x1∈[a,a+1],x2∈[b,b+1],且a,b∈{1,2,3,4,5,6,7,8,9,10,11,12},则a+b=10.