题目内容
14.过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的右焦点F作该双曲线一条渐近线的垂线交此渐近线于点M,若O为坐标原点,△OFM的面积是$\frac{1}{2}{a^2}$,则该双曲线的离心率是( )| A. | 2 | B. | $\sqrt{2}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $\sqrt{5}$ |
分析 依题意,可求得过F(c,0)与一条渐近线bx-ay=0垂直的直线与bx-ay=0的交点M的坐标,利用△OFM的面积是$\frac{1}{2}{a^2}$即可求得此双曲线的离心率
解答 解:设过F(c,0)与一条渐近线bx-ay=0垂直的直线为l,则l的方程为:y=-$\frac{a}{b}$(x-c),
由$\left\{\begin{array}{l}{y=\frac{b}{a}x}\\{y=-\frac{a}{b}(x-c)}\end{array}\right.$得:x=$\frac{{a}^{2}}{c}$,y=$\frac{ab}{c}$,即M($\frac{{a}^{2}}{c}$,$\frac{ab}{c}$),
∵△OAF的面积为$\frac{1}{2}$a2,
∴$\frac{1}{2}$|OF|×yA=$\frac{1}{2}$c×$\frac{ab}{c}$=$\frac{1}{2}$a2,
∴b=a,
∴e=$\frac{c}{a}$=$\sqrt{1+\frac{{b}^{2}}{{a}^{2}}}$=$\sqrt{2}$,
故选:B.
点评 本题考查双曲线的性质,求得M的坐标是关键,考查转化思想与方程思想,属于中档题.

练习册系列答案
相关题目
2.已知点P(x,y)在不等式组$\left\{\begin{array}{l}{x-2≤0}\\{y-1≤0}\\{x+2y-2≥0}\end{array}\right.$,表示的平面区域上运动,则z=x-y的取值范围是( )
| A. | [1,2] | B. | [-2,1] | C. | [-2,-1] | D. | [-1,2] |
9.设$a={2^{0.01}},b=lg2,c=sin\frac{9π}{5}$,则a,b,c的大小关系为( )
| A. | a>b>c | B. | a>c>b | C. | b>a>c | D. | c>a>b |
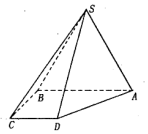 如图,在四棱锥S-ABCD中,平面ABCD⊥平面SAB,侧面SAB为等边三角形,底面ABCD为直角梯形,AB∥CD,AB⊥BC,AB=12,CD=BC=6.
如图,在四棱锥S-ABCD中,平面ABCD⊥平面SAB,侧面SAB为等边三角形,底面ABCD为直角梯形,AB∥CD,AB⊥BC,AB=12,CD=BC=6.