题目内容
4.已知数列{an}的通项公式为${a_n}=6n+5(n∈{N^*})$,数列{bn}是等差数列,且an=bn+bn+1(Ⅰ)求数列{an}的前n项和;
(Ⅱ)求数列{bn}的通项公式.
分析 (Ⅰ)根据等差数列的前n项和公式计算即可,
(Ⅱ)根据递推公式即可求出通项公式
解答 解:(Ⅰ)∵${a_n}=6n+5(n∈{N^*})$
∴${a_{n+1}}-{a_n}=[6(n+1)+5]-(6n+5)=6,\;(n∈{N^*})$
∴数列{an}是等公差为6的等差数列.
又∵a1=11
∴数列{an}的前n项和:${S_n}=\frac{{n({a_1}+{a_n})}}{2}=\frac{n[11+(6n+5)]}{2}=3{n^2}+8n$;
(Ⅱ)∵an=bn+bn+1
∴a1=b1+b2,a2=b2+b3
∴$\left\{\begin{array}{l}{b_1}+{b_2}=11\\{b_2}+{b_3}=17\end{array}\right.$
设数列{bn}的公差为d,
则$\left\{\begin{array}{l}2{b_1}+d=11\\ 2{b_1}+3d=17\end{array}\right.$∴$\left\{\begin{array}{l}{b_1}=4\\ d=3\end{array}\right.$.
∴数列{bn}的通项公式:bn=3n+1.
点评 本题考查了等差数列的通项公式和前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
9.某次数学测验后,数学老师统计了本班学生对选做题的选做情况,得到如表数据:(单位:人)
(I)请完成题中的2×2列联表;并根据表中的数据判断,是否有超过97.5%的把握认为选做“坐标系与参数方程”或“不等式选讲”与性别有关?
(II)经过多次测试后,甲同学发现自己解答一道“坐标系与参数方程”所用的时间为区间[5,7]内一个随机值(单位:分钟),解答一道“不等式选讲”所用的时间为区间[6,8]内一个随机值(单位:分钟),试求甲在考试中选做“坐标系与参数方程”比选做“不等式选讲”所用时间更长的概率.
附表及公式:${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$
| 坐标系与参数方程 | 不等式选讲 | 合计 | |
| 男同学 | 22 | 8 | 30 |
| 女同学 | 8 | 12 | 20 |
| 合计 | 30 | 20 | 50 |
(II)经过多次测试后,甲同学发现自己解答一道“坐标系与参数方程”所用的时间为区间[5,7]内一个随机值(单位:分钟),解答一道“不等式选讲”所用的时间为区间[6,8]内一个随机值(单位:分钟),试求甲在考试中选做“坐标系与参数方程”比选做“不等式选讲”所用时间更长的概率.
附表及公式:${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
16.“x+y=3”是“x=1且y=2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也必要条件 |
14.过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的右焦点F作该双曲线一条渐近线的垂线交此渐近线于点M,若O为坐标原点,△OFM的面积是$\frac{1}{2}{a^2}$,则该双曲线的离心率是( )
| A. | 2 | B. | $\sqrt{2}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $\sqrt{5}$ |
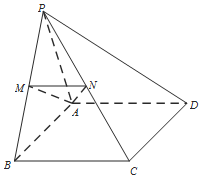 在四棱锥P-ABCD中,△PAB为正三角形,四边形ABCD为矩形,平面PAB⊥平面ABCD,AB=2AD,M,N分别为PB,PC中点.
在四棱锥P-ABCD中,△PAB为正三角形,四边形ABCD为矩形,平面PAB⊥平面ABCD,AB=2AD,M,N分别为PB,PC中点.