题目内容
2.已知点P(x,y)在不等式组$\left\{\begin{array}{l}{x-2≤0}\\{y-1≤0}\\{x+2y-2≥0}\end{array}\right.$,表示的平面区域上运动,则z=x-y的取值范围是( )| A. | [1,2] | B. | [-2,1] | C. | [-2,-1] | D. | [-1,2] |
分析 作出不等式组对应的平面区域,利用z的几何意义进行求解即可.
解答 解:作出不等式组对应的平面区域如图: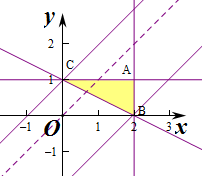
由z=x-y,得y=x-z表示,斜率为1纵截距为-z的一组平行直线,
平移直线y=x-z,当直线y=x-z经过点B时,直线y=x-z的截距最小,此时z最大,
当直线经过点C时,此时直线y=x-z截距最大,z最小.
由$\left\{\begin{array}{l}{x=2}\\{x+2y-2=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=2}\\{y=0}\end{array}\right.$,即B(2,0),此时zmax=2.
由$\left\{\begin{array}{l}{y-1=0}\\{x+2y-2=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=0}\\{y=1}\end{array}\right.$,即C(0,1),此时zmin=0-1=-1.
∴-1≤z≤2,
故选:D.
点评 本题主要考查线性规划的基本应用,利用z的几何意义是解决线性规划问题的关键,注意利用数形结合来解决.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
17.执行如图所示的程序框图,则输出S的值是( )
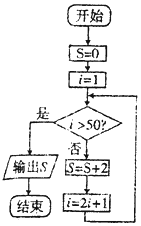

| A. | 10 | B. | 12 | C. | 100 | D. | 102 |
7.已知{an}为等差数列,a1+a3+a5=105,a2+a4+a6=99,则a20等于( )
| A. | 7 | B. | 3 | C. | -1 | D. | 1 |
14.过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的右焦点F作该双曲线一条渐近线的垂线交此渐近线于点M,若O为坐标原点,△OFM的面积是$\frac{1}{2}{a^2}$,则该双曲线的离心率是( )
| A. | 2 | B. | $\sqrt{2}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $\sqrt{5}$ |
11.在四棱锥P-ABCD中,底面是边长为2的菱形,∠DAB=60°,对角线AC与BD相交于点O,PO⊥平面ABCD,PB与平面ABCD所成角为45°,若E是PB的中点,则异面直线DE与PA所成角的余弦值为( )
| A. | $\frac{{3\sqrt{10}}}{20}$ | B. | $\frac{{\sqrt{10}}}{20}$ | C. | $\frac{{2\sqrt{5}}}{5}$ | D. | $\frac{{\sqrt{5}}}{5}$ |
12.已知集合A={x|0<x<2},B={x|x2-1≤0},那么A∪B=( )
| A. | {x|0<x≤1} | B. | {x|-1≤x<2} | C. | {x|-1≤x<0} | D. | {x|1≤x<2} |
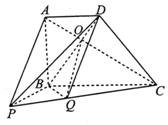 如图,在四棱锥P-ABCD中,ABCD是梯形,AD∥BC,∠ABC=90°,平面PAB⊥平面ABCD,PB⊥AB且AD=AB=BP=$\frac{1}{2}$BC.
如图,在四棱锥P-ABCD中,ABCD是梯形,AD∥BC,∠ABC=90°,平面PAB⊥平面ABCD,PB⊥AB且AD=AB=BP=$\frac{1}{2}$BC.