题目内容
6.已知△ABC的内角A,B,C的对边分别是a,b,c,且$\frac{tanA+tanB}{tanB}=\frac{2c}{b}$.(1)求角A的大小;
(2)若$a=2\sqrt{3}$,求△ABC面积的最大值.
分析 (1)由同角三角函数基本关系,正弦定理,三角形内角和定理,诱导公式化简已知等式可得$cosA=\frac{1}{2}$,结合范围A∈(0,π),可求A的值.
(2)由余弦定理,基本不等式可求bc≤12,进而利用三角形面积公式可求最大值.
解答 (本题满分为12分)
解:(1)因为$\frac{tanA+tanB}{tanB}=\frac{2c}{b}$,
由同角三角函数基本关系和正弦定理得,$\frac{{\frac{sinA}{cosA}+\frac{sinB}{cosB}}}{{\frac{sinB}{cosB}}}=\frac{2sinC}{sinB}$,…(1分)
整理得:$\frac{sin(A+B)}{cosA}=2sinC$,…(3分)
又A+B=π-C,
所以sin(A+B)=sinC,
所以$cosA=\frac{1}{2}$.…(5分)
又A∈(0,π),
所以$A=\frac{π}{3}$.…(6分)
(2)由余弦定理得:$12={b^2}+{c^2}-2bccos\frac{π}{3}$,
即:b2+c2-bc=12,…(8分)
所以12=b2+c2-bc≥2bc-bc=bc,当且仅当$b=c=2\sqrt{3}$时取等号,…(10分)
所以${S_{△ABC}}=\frac{1}{2}bcsin\frac{π}{3}≤\frac{1}{2}×12×\frac{{\sqrt{3}}}{2}=3\sqrt{3}$,
即△ABC面积的最大值为$3\sqrt{3}$.…(12分)
点评 本题主要考查了同角三角函数基本关系,正弦定理,三角形内角和定理,诱导公式,余弦定理,基本不等式,三角形面积公式在解三角形中的应用,考查了转化思想,属于中档题.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目
16.“x+y=3”是“x=1且y=2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也必要条件 |
17.执行如图所示的程序框图,则输出S的值是( )
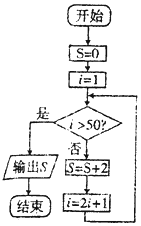

| A. | 10 | B. | 12 | C. | 100 | D. | 102 |
14.过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的右焦点F作该双曲线一条渐近线的垂线交此渐近线于点M,若O为坐标原点,△OFM的面积是$\frac{1}{2}{a^2}$,则该双曲线的离心率是( )
| A. | 2 | B. | $\sqrt{2}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $\sqrt{5}$ |
11.在四棱锥P-ABCD中,底面是边长为2的菱形,∠DAB=60°,对角线AC与BD相交于点O,PO⊥平面ABCD,PB与平面ABCD所成角为45°,若E是PB的中点,则异面直线DE与PA所成角的余弦值为( )
| A. | $\frac{{3\sqrt{10}}}{20}$ | B. | $\frac{{\sqrt{10}}}{20}$ | C. | $\frac{{2\sqrt{5}}}{5}$ | D. | $\frac{{\sqrt{5}}}{5}$ |