题目内容
1.分别求出下列两个程序的运行结果:
分析 首先分别分析两个语句,找到区别,然后分别计算.分别输出i的值即可
解答 解:根据题意,(1)(2)的分别为求s>20时i的值,
区别为(1)先求和再i自加;(2)先自加再求和
对于(1):
s=1+2+3+4+5+6=21>20,
然后i=6+1=7,
输出7;
对于(2):
i=6,
s=1+2+3+4+5+6=21>20,
输出6.
点评 本题考查程序框图,通过对两个不同框图语句的分析分别作答,属于基础题.

练习册系列答案
相关题目
6.在一次考试中,7位同学的数学、物理成绩分数对应如表:
(1)根据上述数据,求出变量y与x的相应系数并说明物理成绩y与数学成绩x之间线性相关关系的强弱
(2)如果物理成绩y与数学成绩x之间有较强的线性相关关系,求y与x的线性回归方程,并估测该班某位同学数学分数是95分时的物理成绩;(系数精确到0.01)
本题参考数据:
$\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}$=700,$\sum_{i=1}^{n}$(xi-$\overline{x}$)(yi-$\overline{y}$)=480,$\sqrt{700}$≈26.5,$\sqrt{336}$≈18.3
参考公式:相关系数r=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sqrt{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}\sum_{i=1}^{n}({y}_{i}-\overline{y})^{2}}}$
对于相关数据系数r的大小,如果r∈[-1,-0.75],那么y与x负相关很强,如果r∈[0.75,1],那么y与x正相关很强,如果r∈(-0.75,-0.30)或r∈(0.30,0.75),那么y与x相关性一般,如果r∈[-0.25,0.25],那么y与x相关性较弱.
回归直线方程:$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$,其中$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.
| 学生 | A | B | C | D | E | F | G |
| 数学(x分) | 60 | 65 | 70 | 75 | 80 | 85 | 90 |
| 物理(y分) | 71 | 77 | 80 | 84 | 87 | 90 | 92 |
(2)如果物理成绩y与数学成绩x之间有较强的线性相关关系,求y与x的线性回归方程,并估测该班某位同学数学分数是95分时的物理成绩;(系数精确到0.01)
本题参考数据:
$\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}$=700,$\sum_{i=1}^{n}$(xi-$\overline{x}$)(yi-$\overline{y}$)=480,$\sqrt{700}$≈26.5,$\sqrt{336}$≈18.3
参考公式:相关系数r=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sqrt{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}\sum_{i=1}^{n}({y}_{i}-\overline{y})^{2}}}$
对于相关数据系数r的大小,如果r∈[-1,-0.75],那么y与x负相关很强,如果r∈[0.75,1],那么y与x正相关很强,如果r∈(-0.75,-0.30)或r∈(0.30,0.75),那么y与x相关性一般,如果r∈[-0.25,0.25],那么y与x相关性较弱.
回归直线方程:$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$,其中$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.
13.已知cosα=$\frac{1}{3}$,则cos2α=( )
| A. | $-\frac{5}{9}$ | B. | $\frac{{\sqrt{6}}}{3}$ | C. | 1 | D. | $-\frac{7}{9}$ |
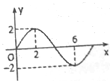 函数f(x)=Asinωx(A>0,ω>0)的部分图象如图所示,则f(1)+f(2)+…+f(2017)=$\sqrt{2}$.
函数f(x)=Asinωx(A>0,ω>0)的部分图象如图所示,则f(1)+f(2)+…+f(2017)=$\sqrt{2}$.