题目内容
已知f(x)=(sinx+cosx)sinx,若f(x1)≤f(x)≤f(x2),对?x∈R成立,则|x1-x2|最小值为( )
A、
| ||
B、
| ||
C、
| ||
| D、π |
考点:三角函数中的恒等变换应用
专题:三角函数的求值,三角函数的图像与性质
分析:由题意可得f(x1)为函数的最小值,f(x2)为函数的最大值,故|x2-x1|的最小值为半个周期,再根据正弦函数的周期性可得结论.
解答:
解:∵f(x)=(sinx+cosx)sinx=
+
sin2x=
sin(2x-
)+
∴T=
=π
∵若f(x1)≤f(x)≤f(x2),对?x∈R成立,
∴可得f(x1)为函数的最小值,f(x2)为函数的最大值,
故|x2-x1|的最小值为半个周期,即
T=
.
故选:C.
| 1-cos2x |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 4 |
| 1 |
| 2 |
∴T=
| 2π |
| 2 |
∵若f(x1)≤f(x)≤f(x2),对?x∈R成立,
∴可得f(x1)为函数的最小值,f(x2)为函数的最大值,
故|x2-x1|的最小值为半个周期,即
| 1 |
| 2 |
| π |
| 2 |
故选:C.
点评:本题主要考查正弦函数的周期性和值域,三角函数中的恒等变换应用,属于基本知识的考查.

练习册系列答案
相关题目
若执行如图的程序框图,则输出的k值是( )


| A、4 | B、5 | C、6 | D、7 |
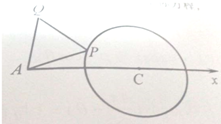 已知半径为2的定圆C外一定点A,且AC=4,在圆上任取一点P,以AP为一边逆时针作等边△APQ,当P在圆上运动时,建立适当的极坐标系,求点Q轨迹的极坐标方程,并转化为直角坐标方程.
已知半径为2的定圆C外一定点A,且AC=4,在圆上任取一点P,以AP为一边逆时针作等边△APQ,当P在圆上运动时,建立适当的极坐标系,求点Q轨迹的极坐标方程,并转化为直角坐标方程.