题目内容
设函数f(x)=axn-lnx-1(n∈N+,n≥2,a>1)是否存在a,使得f(x)存在两个零点x1,x2,若存在,求出a的值,若不存在,请说明理由.
考点:函数零点的判定定理
专题:计算题,导数的综合应用
分析:f(x)=axn-lnx-1的定义域为(0,+∞),令f′(x)=naxn-1-
=
=0得,从而解得.
| 1 |
| x |
| naxn-1 |
| x |
解答:
解:f(x)=axn-lnx-1的定义域为(0,+∞),
令f′(x)=naxn-1-
=
=0得,
x=
,且f(x)在定义域上先减后增,
故f(
)=
+
lnna-1<0,
故a<
;
当n=2时,a=
即成立.
令f′(x)=naxn-1-
| 1 |
| x |
| naxn-1 |
| x |
x=
| n |
| ||
故f(
| n |
| ||
| 1 |
| n |
| 1 |
| n |
故a<
| en-1 |
| n |
当n=2时,a=
| e |
| 2 |
点评:本题考查了导数的综合应用及恒成立问题.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
如图是某几何体的三视图,则该几何体的体积为( )
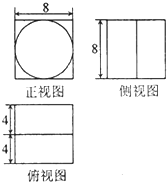

| A、256+128π |
| B、256+64π |
| C、64+64π |
| D、64+32π |
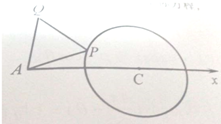 已知半径为2的定圆C外一定点A,且AC=4,在圆上任取一点P,以AP为一边逆时针作等边△APQ,当P在圆上运动时,建立适当的极坐标系,求点Q轨迹的极坐标方程,并转化为直角坐标方程.
已知半径为2的定圆C外一定点A,且AC=4,在圆上任取一点P,以AP为一边逆时针作等边△APQ,当P在圆上运动时,建立适当的极坐标系,求点Q轨迹的极坐标方程,并转化为直角坐标方程.