题目内容
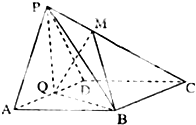 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点,PA=PD;
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点,PA=PD; (1)求证:平面PQB⊥平面PAD;
(2)若平面PAD⊥平面ABCD,PA=AB=2,点M满足
| PC |
| PM |
考点:棱柱、棱锥、棱台的体积,平面与平面垂直的判定
专题:综合题
分析:(1)根据条件和线面垂直的判定定理得:AD⊥平面PQB,再由面面垂直的判断定理证明出平面PQB⊥平面PAD;
(2)根据面面垂直的性质定理的条件得:PQ⊥平面ABCD,再由条件求出PQ、S四边形BCDQ和点M到平面BCDQ的距离,代入三棱锥的体积公式求出四棱锥M-BCDQ的体积.
(2)根据面面垂直的性质定理的条件得:PQ⊥平面ABCD,再由条件求出PQ、S四边形BCDQ和点M到平面BCDQ的距离,代入三棱锥的体积公式求出四棱锥M-BCDQ的体积.
解答:
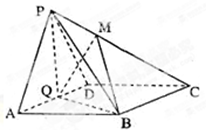 (1)证明:由条件得,
(1)证明:由条件得,
⇒AD⊥平面PQB,
又AD?平面PAD,
所以平面PQB⊥平面PAD…(6分)
(2)解:∵PQ⊥AD,平面PAD⊥平面ABCD=AD,且平面PAD⊥平面ABCD,
∴PQ⊥平面ABCD,
∵PA=AB=2,底面ABCD为菱形,∠BAD=60°,Q为AD的中点,PA=PD,
∴PQ=
,S四边形BCDQ=
×(1+2)×
=
,
由
=3
得,点M到平面BCDQ的距离是
PQ,
∴VM-BCDQ=
S四边形BCDQ•
PQ=1…(12分)
 (1)证明:由条件得,
(1)证明:由条件得,
|
又AD?平面PAD,
所以平面PQB⊥平面PAD…(6分)
(2)解:∵PQ⊥AD,平面PAD⊥平面ABCD=AD,且平面PAD⊥平面ABCD,
∴PQ⊥平面ABCD,
∵PA=AB=2,底面ABCD为菱形,∠BAD=60°,Q为AD的中点,PA=PD,
∴PQ=
| 3 |
| 1 |
| 2 |
| 3 |
3
| ||
| 2 |
由
| PC |
| PM |
| 2 |
| 3 |
∴VM-BCDQ=
| 1 |
| 3 |
| 2 |
| 3 |
点评:本题考查了线面垂直的判定定理、面面垂直的判断定理和性质定理的综合应用,以及三棱锥的体积公式的应用.

练习册系列答案
相关题目
下列命题中,正确的是( )
| A、如果两条平行直线中的一条与平面α平行,那么另一条也与平面α平行 |
| B、若两个平面垂直,则一个平面内的任一条直线必垂直于另一个平面 |
| C、若直线l与平面α平行,则l与平面α内的任意一条直线都没有公共点 |
| D、垂直于同一平面的两个平面互相平行 |
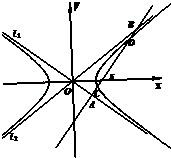 双曲线
双曲线 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD⊥底面ABCD,E,F分别为PA,BD中点,PA=PD=AD=2.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD⊥底面ABCD,E,F分别为PA,BD中点,PA=PD=AD=2.