题目内容
已知函数f（x）=|x-a|．
（1）若不等式f（x）≤4的解集为{x|-2≤x≤6}，求实数a的值；
（2）在（1）的条件下，若f（x）-f（x+5）≤m对一切实数x恒成立，求实数m的取值范围．
（1）若不等式f（x）≤4的解集为{x|-2≤x≤6}，求实数a的值；
（2）在（1）的条件下，若f（x）-f（x+5）≤m对一切实数x恒成立，求实数m的取值范围．
考点：绝对值不等式的解法
专题：不等式的解法及应用
分析：（1）由不等式f（x）≤4，求得 a-4≤x≤a+4．再根据不等式f（x）≤4的解集为{x|-2≤x≤6}，可得a-4=-2，且a+4=6，由此求得a的值．
（2）由题意可得|x-2|-|x+3|的最大值小于或等于m，而|x-2|-|x+3|≤|（x-2）-（x+3）|=5，可得m≥5．
（2）由题意可得|x-2|-|x+3|的最大值小于或等于m，而|x-2|-|x+3|≤|（x-2）-（x+3）|=5，可得m≥5．
解答：
解：（1）不等式f（x）≤4，即|x-a|≤4，即-4≤x-a≤4，求得 a-4≤x≤a+4．
再根据不等式f（x）≤4的解集为{x|-2≤x≤6}，可得a-4=-2，且a+4=6，求得 a=2．
（2）在（1）的条件下，若f（x）-f（x+5）≤m对一切实数x恒成立，即|x-2|-|x+3|≤m恒成立，
故|x-2|-|x+3|的最大值小于或等于m．
而|x-2|-|x+3|≤|（x-2）-（x+3）|=5，∴m≥5，即m的范围为[5，+∞）．
再根据不等式f（x）≤4的解集为{x|-2≤x≤6}，可得a-4=-2，且a+4=6，求得 a=2．
（2）在（1）的条件下，若f（x）-f（x+5）≤m对一切实数x恒成立，即|x-2|-|x+3|≤m恒成立，
故|x-2|-|x+3|的最大值小于或等于m．
而|x-2|-|x+3|≤|（x-2）-（x+3）|=5，∴m≥5，即m的范围为[5，+∞）．
点评：本题主要考查绝对值三角不等式，绝对值不等式的解法，函数的恒成立问题，体现了转化的数学思想，属于基础题．
练习册系列答案
相关题目
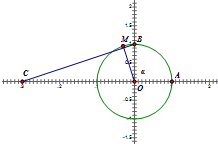如图，A、B是单位圆与x轴、y轴正半轴的交点，点M在单位圆上，∠AOM=α（0＜α＜π），点C（-3，0），若BC⊥OM，则sin（2α-| π |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若函数f（x）=sin2x-cos2x+sin2x-m在[0，
]上有零点，则实数m的取值范围为（ ）
| π |
| 4 |
A、[-1，
| ||
| B、[-1，1] | ||
C、[1，
| ||
D、[-
|
以圆 （x-1）2+y2=2的圆心为抛物线的焦点，且顶点为坐标原点的抛物线方程为（ ）
| A、y2=4x |
| B、y2=2x |
| C、x2=4y |
| D、x2=2y |
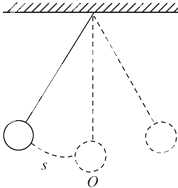如图，单摆从某点开始来回摆动，离开平衡位置O的距离s cm和时间t s的函数关系式为s=6sin（2πt+| π |
| 6 |
| A、2π s |
| B、π s |
| C、0.5 s |
| D、1 s |
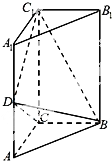如图，三棱柱ABC-A1B1C1中，侧棱垂直底面，∠ACB=90°，AC=2，BC=4，AA1=4，D是棱AA1的中点．