题目内容
已知倾斜角为45°的直线l通过抛物线y2=4x的焦点F，且与抛物线相交于A、B两点，则弦AB的长为（ ）
| A、16 | B、18 | C、8 | D、6 |
考点：双曲线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：先根据题意写出直线的方程，再将直线的方程与抛物线y2=4x的方程组成方程组，消去y得到关于x的二次方程，最后利用根与系数的关系结合抛物线的定义即可求线段AB的长．
解答：
解：设A（x1，y1），B（x2，y2），A，B到准线的距离分别为dA，dB，
由抛物线的定义可知|AF|=dA=x1+1，|BF|=dB=x2+1，于是|AB|=|AF|+|BF|=x1+x2+2．
由已知得抛物线的焦点为F（1，0），斜率k=tan45°=1，所以直线AB方程为y=x-1．
将y=x-1代入方程y2=4x，得（x-1）2=4x，化简得x2-6x+1=0．
由求根公式得x1+x2=6，于是|AB|=|AF|+|BF|=x1+x2+2=8．
故选：C．
由抛物线的定义可知|AF|=dA=x1+1，|BF|=dB=x2+1，于是|AB|=|AF|+|BF|=x1+x2+2．
由已知得抛物线的焦点为F（1，0），斜率k=tan45°=1，所以直线AB方程为y=x-1．
将y=x-1代入方程y2=4x，得（x-1）2=4x，化简得x2-6x+1=0．
由求根公式得x1+x2=6，于是|AB|=|AF|+|BF|=x1+x2+2=8．
故选：C．
点评：本题主要考查了抛物线的应用以及直线与圆锥曲线的综合问题和方程的思想，属中档题．
练习册系列答案
名校课堂系列答案
相关题目
已知x＞0，y＞0，
+
=1．若x+2y＞m2-2m恒成立，则实数m的取值范围是（ ）
| 2 |
| x |
| 1 |
| y |
| A、m≥4或m≤-2 |
| B、-2＜m＜4 |
| C、m≥2或m≤-4 |
| D、-4＜m＜2 |
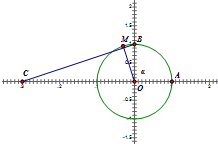如图，A、B是单位圆与x轴、y轴正半轴的交点，点M在单位圆上，∠AOM=α（0＜α＜π），点C（-3，0），若BC⊥OM，则sin（2α-| π |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
一个不透明的盒子里有质地、大小完全相同的5个球，编号分别为1，2，3，4，5，甲、乙两人玩一种游戏：甲先摸出一个球，记下编号，放回后乙再摸一个球，记下编号，如果两个编号的和为偶数算甲赢，否则算乙赢．那么甲赢的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
| D、以上均不对 |
等比数列{an}中，a3、a15是方程x2-6x+8=0的两根，则a1a9a17=（ ）
A、16
| ||||
B、-16
| ||||
C、16
| ||||
| D、64 |
若函数f（x）=sin2x-cos2x+sin2x-m在[0，
]上有零点，则实数m的取值范围为（ ）
| π |
| 4 |
A、[-1，
| ||
| B、[-1，1] | ||
C、[1，
| ||
D、[-
|
以圆 （x-1）2+y2=2的圆心为抛物线的焦点，且顶点为坐标原点的抛物线方程为（ ）
| A、y2=4x |
| B、y2=2x |
| C、x2=4y |
| D、x2=2y |