题目内容
求函数y=asin2x+2sinx-
,x∈[
,
]的值域.
| 1 |
| 2 |
| π |
| 6 |
| 5π |
| 6 |
考点:三角函数的最值
专题:分类讨论,三角函数的图像与性质
分析:讨论a=0时,y的值域是什么,a≠0时,函数y的值域是什么,求出答案来.
解答:
解:∵函数y=asin2x+2sinx-
,
∴①当a=0时,y=2sinx-
,
∵x∈[
,
],
∴sinx∈[
,1],
∴y=2sinx-
∈[
,
];
②当a≠0时,
y=a(sin2x+
sinx+
)-
-
=a(sinx+
)2-
-
,
(i)若a>0,则函数y的最大值是ymax=a+2-
=a+
,
y的最小值是ymin=
a+1-
=
a+
,
∴
a+
≤y≤a+
;
(ii)若-1≤a<0,则
≤-1,
函数y的最大值是ymax=a+2-
=a+
,
y的最小值是ymin=
a+1-
=
a+
,
∴
a+
≤y≤a+
(iii)若-2≤a<-1,则-1<
≤-
,
函数y的最大值是ymax=-
-
,
y的最小值是ymin=
a+1-
=
a+
;
∴
a+
≤y≤-
-
(iv)若a<-2,则-
<
<0,
函数y的最大值是ymax=a+
,
y的最小值是ymin=
a+1-
=
a+
;
∴
a+
≤y≤a+
综上,a=0时,y的值域是[
,
],
a>0时,y的值域是[
a+
,a+
];
-1≤a<0时,y的值是[
a+
,a+
]
-2≤a<-1时,y的值是[
a+
,-
-
]
a<-2时,y的值是[
a+
;a+
].
| 1 |
| 2 |
∴①当a=0时,y=2sinx-
| 1 |
| 2 |
∵x∈[
| π |
| 6 |
| 5π |
| 6 |
∴sinx∈[
| 1 |
| 2 |
∴y=2sinx-
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
②当a≠0时,
y=a(sin2x+
| 2 |
| a |
| 1 |
| a2 |
| 1 |
| a |
| 1 |
| 2 |
| 1 |
| a |
| 1 |
| a |
| 1 |
| 2 |
(i)若a>0,则函数y的最大值是ymax=a+2-
| 1 |
| 2 |
| 3 |
| 2 |
y的最小值是ymin=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
∴
| 1 |
| 4 |
| 1 |
| 2 |
| 3 |
| 2 |
(ii)若-1≤a<0,则
| 1 |
| a |
函数y的最大值是ymax=a+2-
| 1 |
| 2 |
| 3 |
| 2 |
y的最小值是ymin=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
∴
| 1 |
| 4 |
| 1 |
| 2 |
| 3 |
| 2 |
(iii)若-2≤a<-1,则-1<
| 1 |
| a |
| 1 |
| 2 |
函数y的最大值是ymax=-
| 1 |
| a |
| 1 |
| 2 |
y的最小值是ymin=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
∴
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| a |
| 1 |
| 2 |
(iv)若a<-2,则-
| 1 |
| 2 |
| 1 |
| a |
函数y的最大值是ymax=a+
| 3 |
| 2 |
y的最小值是ymin=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
∴
| 1 |
| 4 |
| 1 |
| 2 |
| 3 |
| 2 |
综上,a=0时,y的值域是[
| 1 |
| 2 |
| 3 |
| 2 |
a>0时,y的值域是[
| 1 |
| 4 |
| 1 |
| 2 |
| 3 |
| 2 |
-1≤a<0时,y的值是[
| 1 |
| 4 |
| 1 |
| 2 |
| 3 |
| 2 |
-2≤a<-1时,y的值是[
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| a |
| 1 |
| 2 |
a<-2时,y的值是[
| 1 |
| 4 |
| 1 |
| 2 |
| 3 |
| 2 |
点评:本题考查了分类讨论思想的应用问题,也考查了三角函数的图象与性质的应用问题,是易错题.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
设m,n表示不同直线,α,β表示不同平面,则下列命题中正确的是( )
| A、若m∥α,m∥n,则n∥α |
| B、若m?α,n?β,n∥α,则α∥β |
| C、若α∥β,m∥α,m∥n,则n∥β |
| D、若α∥β,m∥α,n∥m,n?β,则n∥β |
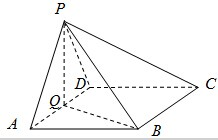 在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点,若PA=PD.
在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点,若PA=PD.