题目内容

已知一正四棱锥S-ABCD的棱长都等于a，求侧面与底面所成二面角的余弦值．
考点：直线与平面所成的角
专题：空间位置关系与距离,空间角
分析：正四棱锥S-ABCD的所有棱长均为a，过S作SO⊥面ABCD，垂足为O，过O作OE⊥BC，交BC于E，连结SE，
则由三垂线定理知∠SEO是侧面SBC与底面ABCD所成二面角的平面角，由此能求出结果．
解答： 解：如图，

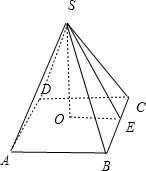
∵正四棱锥S-ABCD的所有棱长均为a，
过S作SO⊥面ABCD，垂足为O，
过O作OE⊥BC，交BC于E，连结SE，
则由三垂线定理知：
∠SEO是侧面SBC与底面ABCD所成二面角的平面角，
由题意知SE=
a2-(
a
2
)2
=
3
2
a，OE=
a
2
，
∴cos∠SEO=
OE
SE
=
a
2
3
2
a
=
3
3
．
故答案为：
3
3
．
点评：本题考查二面角的余弦值的求法，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
相关题目
下列四组函数中，表示相等函数的一组是（　　）
A、y=x与y=
x2
x
B、y=±x与y=
x2
C、y=x与y=
3x3
D、y=|x|与y=(
x
)2
已知直角三角形ABE，AB⊥BE，AB=2BE=4，C，D分别是AB，AE上的中点，且CD∥BE，将△ACD沿CD折起到位置A1CD，使平面A1CD与平面BCD所成的二面角A1-CD-B的大小为θ，．
（1）若θ=
π
3
，求直线A1E与平面BCD所成的角的正切值；
（2）已知G为A1E的中点，若BG⊥A1D，求cosθ的取值．
随机向边长为5，5，6的三角形中投一点P，则点P到三个顶点的距离都不小于1的概率是
 
．
求证：两条平行线中的一条与已知平面相交，则另一条也与该平面相交．
求函数y=asin2x+2sinx-
1
2
，x∈[
π
6
，
5π
6
]的值域．
已知fn（x）=（1+x）n．
（1）若f2014（x）=a0+a1x+…+a2014x2014，求a0+a2+…+a2014的值；
（2）若g（x）=f6（x）+2f7（x）+3f8（x），求g（x）的展开式中含x6的项的系数．
已知⊙C：x2+y2-2ax-2（8-a）y+4a+12=0（a∈R），点P（2，0）．
（1）判断点P与⊙C的位置关系；
（2）如果过点P的直线l与⊙C有两个交点M、N，求证：|PM|•|PN|为定值．
已知函数f（x）=a+
1
2x-1
是奇函数，
（Ⅰ）求实数a的值，并证明你的结论；
（Ⅱ）求函数y=f（x）的值域．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网