题目内容
已知f(x)=ax3+bx2+c的图象经过点(0,1),且在x=1处的切线方程是y=x.
(1)求y=f(x)的解析式;
(2)求y=f(x)的单调递增区间.
(1)求y=f(x)的解析式;
(2)求y=f(x)的单调递增区间.
考点:利用导数研究函数的单调性,利用导数研究曲线上某点切线方程
专题:综合题,导数的概念及应用
分析:(1)由f(x)=ax3+bx2+c的图象经过点(0,1),得c=1,由导数的几何意义得f′(1)=3a+2b=1①,易求切点(1,1),代入函数解析式可得a+b+1=1②,联立可解;
(2)解不等式f′(x)>0可得增区间,注意写成区间形式;
(2)解不等式f′(x)>0可得增区间,注意写成区间形式;
解答:
解:(1)f(x)=ax3+bx2+c的图象经过点(0,1),则c=1,
f′(x)=3ax2+2bx,f′(1)=3a+2b=1①,
切点为(1,1),则f(x)=ax3+bx2+c的图象经过点(1,1),
得a+b+1=1②,联立①②解得a=1,b=-1,
∴f(x)=x3-x2+1;
(2)f′(x)=3x2-2x>0得x<0或x>
,
单调递增区间为(-∞,0),(
,+∞).
f′(x)=3ax2+2bx,f′(1)=3a+2b=1①,
切点为(1,1),则f(x)=ax3+bx2+c的图象经过点(1,1),
得a+b+1=1②,联立①②解得a=1,b=-1,
∴f(x)=x3-x2+1;
(2)f′(x)=3x2-2x>0得x<0或x>
| 2 |
| 3 |
单调递增区间为(-∞,0),(
| 2 |
| 3 |
点评:该题考查导数的几何意义、利用导数研究函数的单调性,属基础题,正确理解导数的几何意义及单调性与导数的关系是解题关键.

练习册系列答案
相关题目
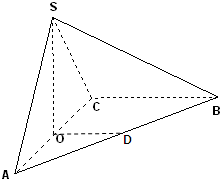 在三棱锥S-ABC中,平面SAC⊥平面ABC,且△SAC是正三角形,O是AC的中点,D是AB的中点.
在三棱锥S-ABC中,平面SAC⊥平面ABC,且△SAC是正三角形,O是AC的中点,D是AB的中点.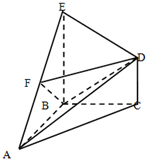 如图,在几何体ABCDE中,BE⊥平面ABC,CD∥BE,△ABC是等腰直角三角形,∠ABC=90°,且BE=AB=2,CD=1,点F是AE的中点.建立适当的空间直角坐标系,利用空间向量方法解答以下问题:
如图,在几何体ABCDE中,BE⊥平面ABC,CD∥BE,△ABC是等腰直角三角形,∠ABC=90°,且BE=AB=2,CD=1,点F是AE的中点.建立适当的空间直角坐标系,利用空间向量方法解答以下问题: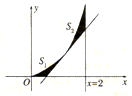 已知l1为函数f(x)=x2(x∈[0,2])在P(t,t2)(t∈(0,2))处的切线,l2为x=2,f(x),l1,l2与x轴所围成的图形如图所示.
已知l1为函数f(x)=x2(x∈[0,2])在P(t,t2)(t∈(0,2))处的切线,l2为x=2,f(x),l1,l2与x轴所围成的图形如图所示. 在长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E为BB1中点.
在长方体ABCD-A1B1C1D1中,AB=BC=1,AA1=2,E为BB1中点.