题目内容
若关于x的方程x2+2kx+3k=0的两相异实根都在（-1，3）内，则k的取值范围是（ ）
| A、k≥3或k≤0 |
| B、k＜-1 |
| C、k＞0 |
| D、（-1，0） |
考点：一元二次方程的根的分布与系数的关系
专题：不等式的解法及应用
分析：令f（x）=x2+2kx+3k，由关于x的方程x2+2kx+3k=0的两相异实根都在（-1，3）内，可得f（-1）=0，f（3）＞0，f（-
）=f（-k）＜0同时成立，由此求得k的取值范围．
| b |
| 2a |
解答：
解：令f（x）=x2+2kx+3k，
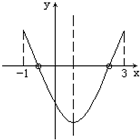
其图象与x轴交点的横坐标（零点）就是方程f（x）=0的解，
由y=f（x）的图象可知，要使函数的两个零点都在（-1，3）内，
只需f（-1）＞0，f（3）＞0，f（-
）=f（-k）＜0，同时成立，
解得-1＜k＜0，故k∈（-1，0）．
故选D
解：令f（x）=x2+2kx+3k，其图象与x轴交点的横坐标（零点）就是方程f（x）=0的解，
由y=f（x）的图象可知，要使函数的两个零点都在（-1，3）内，
只需f（-1）＞0，f（3）＞0，f（-
| b |
| 2a |
解得-1＜k＜0，故k∈（-1，0）．
故选D
点评：本题考查一元二次方程根的分布与系数的关系，由条件得到f（-1）=0，f（3）＞0，f（-
）=f（-k）＜0 同时
成立，是解题的关键．
| b |
| 2a |
成立，是解题的关键．
练习册系列答案
相关题目
已知A，B，C为圆O上三点，线段CO的延长线与线段AB有交点，若
=m
+n
，则m+n的范围是（ ）
| OC |
| OA |
| OB |
| A、（0，1） |
| B、（1，+∞） |
| C、（-1，0） |
| D、（-∞，-1） |
二次函数y=a（a+1）x2-（2a+1）x+1，当a=1，2，3，…，n，…时，其图象在x轴上截得的弦长依次为d1，d2，…，dn，…，则d1+d2+…+dn为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
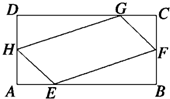如图所示，在矩形ABCD中，已知AB=a，BC=b（b＜a），AB，AD，CD，CB上分别截取AE，AH，CG，CF都等于x，记四边形EFGH的面积为f（x）．