题目内容
已知圆的圆心为C（-1，3），直线3x+4y-7=0被圆截得的弦长为
，则圆的方程为（ ）
8
| ||
| 5 |
| A、（x+1）2+（y-3）2=4 |
| B、（x-1）2+（y+3）2=4 |
| C、（x+1）2+（y+3）2=4 |
| D、（x-1）2+（y-3）2=4 |
考点：直线与圆的位置关系
专题：计算题
分析：设圆的半径为R，弦长为|AB|，利用点到直线的距离公式求出圆心C到直线3x+4y-7=0的距离，即为弦心距d，根据垂径定理由垂直得中点，由弦长的一半，弦心距d，利用勾股定理即可求出圆的半径R，由圆心坐标和求出的R，写出圆的标准方程即可．
解答：
解：设圆的半径为R，弦长|AB|=
，
∵圆心C（-1，3）到直线3x+4y-7=0的距离d=
=
，
∴圆的半径R=
=
=2
则所求圆的方程为：（x+1）2+（y-3）2=4．
故选A
8
| ||
| 5 |
∵圆心C（-1，3）到直线3x+4y-7=0的距离d=
| |-3+12-7| |
| 5 |
| 2 |
| 5 |
∴圆的半径R=
d2+(
|
(
|
则所求圆的方程为：（x+1）2+（y-3）2=4．
故选A
点评：此题考查了直线与圆的位置关系，涉及的知识有：圆的标准方程，点到直线的距离公式，垂径定理，以及勾股定理，当直线与圆相交时，常常根据垂径定理由垂直得中点，然后由弦长的一半，圆的半径及弦心距构造直角三角形，利用勾股定理来解决问题．
练习册系列答案
阅读快车系列答案
相关题目
设椭圆
+y2=1的左、右焦点分别为F1，F2，M为椭圆上异于长轴端点的一点，∠F1MF2=2θ，△MF1F2的内心为I，则|MI|COSθ=（ ）
| x2 |
| 4 |
A、2-
| ||||
B、
| ||||
C、
| ||||
D、
|
已知某个几何体的三视图如右，那么可得这个几何体的体积是（ ）
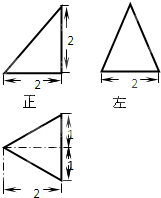
A、
| ||
B、
| ||
C、
| ||
D、
|
已知不等式组
所表示的平面区域为面积等于1的三角形，则实数k的值为（ ）
|
| A、-1 | ||
B、-
| ||
C、
| ||
| D、1 |