题目内容
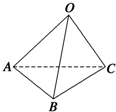 如图所示,已知空间四边形OABC中,OB=OC,且∠AOB=∠AOC=
如图所示,已知空间四边形OABC中,OB=OC,且∠AOB=∠AOC=| π |
| 3 |
| OA |
| BC |
考点:平面向量数量积的运算
专题:平面向量及应用,空间向量及应用
分析:利用向量三角形法则、数量积运算性质即可得出.
解答:
解:∵
=
-
,OB=OC,
∴
•
=
•(
-
)
=
•
-
•
=|
||
|cos
-|
||
|cos
=0,
故答案为:0.
| BC |
| OC |
| OB |
∴
| OA |
| BC |
| OA |
| OC |
| OB |
=
| OA |
| OC |
| OA |
| OB |
=|
| OA |
| OC |
| π |
| 3 |
| OA |
| OB |
| π |
| 3 |
=0,
故答案为:0.
点评:本题考查了向量三角形法则、数量积运算性质,考查了计算能力,属于基础题.

练习册系列答案
相关题目
| OA, |
| OB |
| OA |
| OB |
| OM |
| OA |
| ON |
| OB |
| MN |
| 2 |
| 7 |
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
若函数f(x)唯一的一个零点同时在区间(2,16),(2,8),(2,4)内,那么下列命题中正确的是( )
| A、f(x)在区间(2,3)内有零点 |
| B、f(x)在区间(2,3)或(3,4)内有零点 |
| C、f(x)在区间(3,16)内无零点 |
| D、f(x)在区间(4,16)内无零点 |
已知偶函数f(x)满足:当x1,x2∈(0,+∞)时,(x1-x2)[f(x1)-f(x2)]>0恒成立.设a=f(-4),b=f(1),c=f(3),则a,b,c的大小关系为( )
| A、a<b<c |
| B、b<a<c |
| C、b<c<a |
| D、c<b<a |
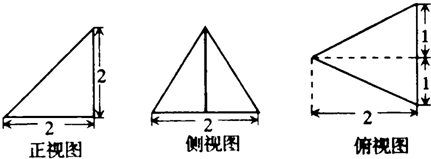
已知某个几何体的三视图如图所示.根据图中标出的尺寸(单位:cm).可得这个几何体的体积是 cm3.
( )
( )

A、
| ||||
B、
| ||||
C、
| ||||
| D、4 |
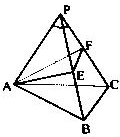 如图,三棱锥P-ABC中,∠APB=∠BPC=∠CPA=30°PA=PB=PC=a,E,F分别为PB,PC上的点,则△AEF周长的最小值等于 ( )
如图,三棱锥P-ABC中,∠APB=∠BPC=∠CPA=30°PA=PB=PC=a,E,F分别为PB,PC上的点,则△AEF周长的最小值等于 ( )