题目内容
已知等比数列{an}的前n项和为Sn=k•2n-1+1,
(1)求S5的值;
(2)若数列{bn}满足bn=log2|an|,求数列{bn}的前n项和Tn.
(1)求S5的值;
(2)若数列{bn}满足bn=log2|an|,求数列{bn}的前n项和Tn.
考点:数列的求和,等比数列的前n项和
专题:等差数列与等比数列
分析:(1)由已知得a1=S1=k+1,a2=S2-S1=k,a3=S3-S1=2k,从而k2=(k+1)•2k,由此求出k,从而能求出S5.
(2)由an=(-1)•2n-1=-2n-1,得bn=log2|an|=n-1,由此能求出Tn.
(2)由an=(-1)•2n-1=-2n-1,得bn=log2|an|=n-1,由此能求出Tn.
解答:
解:(1)∵等比数列{an}的前n项和为Sn=k•2n-1+1,
∴a1=S1=k+1,
a2=S2-S1=(2k+1)-(k+1)=k,
a3=S3-S1=(4k+1)-(2k+1)=2k,
∵{an}是等比数列,∴a22=a1a3,
∴k2=(k+1)•2k,解得k=0(舍)或k=-2,
∴S5=(-2)•24+1=-31.
(2)由(1)得a1=-1,a2=-2,a3=-4,
∴an=(-1)•2n-1=-2n-1,
∴bn=log2|an|=n-1,
∴Tn=(1+2+3+…+n)-n
=
-1
=
.
∴a1=S1=k+1,
a2=S2-S1=(2k+1)-(k+1)=k,
a3=S3-S1=(4k+1)-(2k+1)=2k,
∵{an}是等比数列,∴a22=a1a3,
∴k2=(k+1)•2k,解得k=0(舍)或k=-2,
∴S5=(-2)•24+1=-31.
(2)由(1)得a1=-1,a2=-2,a3=-4,
∴an=(-1)•2n-1=-2n-1,
∴bn=log2|an|=n-1,
∴Tn=(1+2+3+…+n)-n
=
| n(n+1) |
| 2 |
=
| n2-n |
| 2 |
点评:本题考查数列的前n项和的求法,是中档题,解题时要认真审题,注意等差数列和等比数列的性质、分组求和法的合理运用.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
若不等式|ax+1|≤3 的解集为{x|-2≤x≤1}.则a的值为( )
| A、2 | ||
| B、1 | ||
C、
| ||
| D、-2 |
某空间几何体的三视图如图所示,则该几何体的体积是( )


| A、4 | B、5 | C、6 | D、7 |
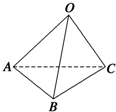 如图所示,已知空间四边形OABC中,OB=OC,且∠AOB=∠AOC=
如图所示,已知空间四边形OABC中,OB=OC,且∠AOB=∠AOC= 某高校在今年的自主招生考试成绩中随机抽取100名考生的笔试成绩,分为5组制出频率分布直方图如图所示.
某高校在今年的自主招生考试成绩中随机抽取100名考生的笔试成绩,分为5组制出频率分布直方图如图所示.