题目内容
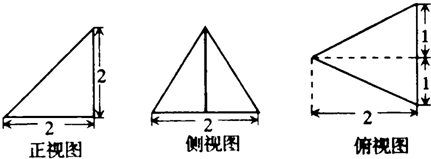
已知某个几何体的三视图如图所示.根据图中标出的尺寸(单位:cm).可得这个几何体的体积是 cm3.
( )
( )

A、
| ||||
B、
| ||||
C、
| ||||
| D、4 |
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:由三视图知几何体是一个三棱锥,三棱锥的底面是一个底边是2,高是2的三角形,三棱锥的高是2,根据三棱锥的体积公式得到结果.
解答:
解:原几何体为底面是高为2,底边长是2的三角形的三棱锥,该三棱锥的高是2,
所以体积是
×
×2×2×2=
.
故选:A.
所以体积是
| 1 |
| 3 |
| 1 |
| 2 |
| 4 |
| 3 |
故选:A.
点评:本题考查由三视图还原几何体并且看出几何体各个部分的长度,本题解题的关键是要求体积需要求出几何体的底面面积和高.本题是一个基础题.

练习册系列答案
 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
已知函数f(x)=msinx-cosx,若x0是函数f(x)的一个极值点,且cos2x0=-
,则m的值为( )
| 3 |
| 5 |
| A、1 | B、±1 | C、2 | D、±2 |
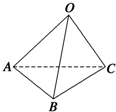 如图所示,已知空间四边形OABC中,OB=OC,且∠AOB=∠AOC=
如图所示,已知空间四边形OABC中,OB=OC,且∠AOB=∠AOC=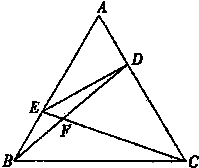 如图,在正三角形ABC中,点D,E分别在边AC,AB上,且AD=
如图,在正三角形ABC中,点D,E分别在边AC,AB上,且AD= 某高校在今年的自主招生考试成绩中随机抽取100名考生的笔试成绩,分为5组制出频率分布直方图如图所示.
某高校在今年的自主招生考试成绩中随机抽取100名考生的笔试成绩,分为5组制出频率分布直方图如图所示.