题目内容
已知偶函数f(x)满足:当x1,x2∈(0,+∞)时,(x1-x2)[f(x1)-f(x2)]>0恒成立.设a=f(-4),b=f(1),c=f(3),则a,b,c的大小关系为( )
| A、a<b<c |
| B、b<a<c |
| C、b<c<a |
| D、c<b<a |
考点:奇偶性与单调性的综合
专题:函数的性质及应用
分析:由当x1,x2∈(0,+∞)时,(x1-x2)[f(x1)-f(x2)]>0恒成立,得函数为增函数,利用函数的单调性进行比较即可.
解答:
解:∵当x1,x2∈(0,+∞)时,(x1-x2)[f(x1)-f(x2)]>0恒成立,
∴当x∈(0,+∞)时,函数f(x)为增函数,
∵f(x)是偶函数,
∴f(1)<f(3)<f(4),
即f(1)<f(3)<f(-4),
故b<c<a,
故选:B
∴当x∈(0,+∞)时,函数f(x)为增函数,
∵f(x)是偶函数,
∴f(1)<f(3)<f(4),
即f(1)<f(3)<f(-4),
故b<c<a,
故选:B
点评:本题主要考查函数值的大小比较,根据条件判断函数的单调性,利用函数奇偶性和单调性之间的关系是解决本题的关键.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
若不等式|ax+1|≤3 的解集为{x|-2≤x≤1}.则a的值为( )
| A、2 | ||
| B、1 | ||
C、
| ||
| D、-2 |
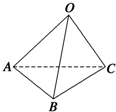 如图所示,已知空间四边形OABC中,OB=OC,且∠AOB=∠AOC=
如图所示,已知空间四边形OABC中,OB=OC,且∠AOB=∠AOC=