题目内容
直线3x-4y+12=0与坐标轴的交点是圆C一条直径的两端点
(Ⅰ)求圆C的方程;
(Ⅱ)圆C的弦AB长度为
且过点(1,
),求弦AB所在直线的方程.
(Ⅰ)求圆C的方程;
(Ⅱ)圆C的弦AB长度为
| 21 |
| 1 |
| 2 |
考点:直线和圆的方程的应用
专题:直线与圆
分析:(1)由题意可得,A(0,3)B(-4,0),AB的中点(-2,
)为圆的圆心,直径AB=5,从而可利用圆的标准方程求解;
(2)圆C的弦AB长度为
,所以圆心到直线的距离为1,设直线方程为y-
=k(x-1),利用点到直线的距离公式,即可求弦AB所在直线的方程.
| 1 |
| 2 |
(2)圆C的弦AB长度为
| 21 |
| 1 |
| 2 |
解答:
解:(Ⅰ)由题意可得,A(0,3)B(-4,0)
AB的中点(-2,
)为圆的圆心,直径AB=5
以线段AB为直径的圆的方程(x+2)2+(y-
)2=6.25;
(Ⅱ)圆C的弦AB长度为
,所以圆心到直线的距离为1,
设直线方程为y-
=k(x-1),即kx-y-k+
=0,
所以
=1,所以k=0或-
,
所以弦AB所在直线的方程为y=
或3x+4y-5=0.
AB的中点(-2,
| 1 |
| 2 |
以线段AB为直径的圆的方程(x+2)2+(y-
| 1 |
| 2 |
(Ⅱ)圆C的弦AB长度为
| 21 |
设直线方程为y-
| 1 |
| 2 |
| 1 |
| 2 |
所以
| |-3k-1| | ||
|
| 3 |
| 4 |
所以弦AB所在直线的方程为y=
| 1 |
| 2 |
点评:本题主要考查了由圆的圆心及圆的直径求解圆的方程,圆的标准方程的应用,属于基本方法的应用.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
 如图,M、N是焦点为F的抛物线y2=2px(p>0)上两个不同的点,且线段MN中点A的横坐标为
如图,M、N是焦点为F的抛物线y2=2px(p>0)上两个不同的点,且线段MN中点A的横坐标为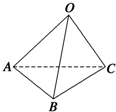 如图所示,已知空间四边形OABC中,OB=OC,且∠AOB=∠AOC=
如图所示,已知空间四边形OABC中,OB=OC,且∠AOB=∠AOC=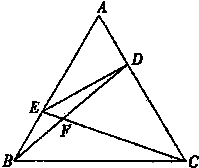 如图,在正三角形ABC中,点D,E分别在边AC,AB上,且AD=
如图,在正三角形ABC中,点D,E分别在边AC,AB上,且AD=