题目内容
已知f(x)的定义域是R,且f(x+2)=f(x+1)-f(x),f(1)=lg3-lg2,f(2)=lg3+lg5,则f(2009)= .
考点:对数的运算性质,抽象函数及其应用
专题:函数的性质及应用
分析:由f(x+2)=f(x+1)-f(x),f(1)=lg3-lg2,f(2)=lg3+lg5,可得f(3)=f(2)-f(1)=lg5+lg2=1,f(4)=f(3)-f(2)=lg2-lg3,f(5)=f(4)-f(3)=-lg15.f(6)=f(5)-f(4)=-1,f(7)=f(6)-f(5)=lg3-lg2=f(1),
…,f(n+6)=f(n),即可得出.
…,f(n+6)=f(n),即可得出.
解答:
解:∵f(x+2)=f(x+1)-f(x),f(1)=lg3-lg2,f(2)=lg3+lg5,
∴f(3)=f(2)-f(1)=lg5+lg2=1,
∴f(4)=f(3)-f(2)=lg2-lg3,
f(5)=f(4)-f(3)=-lg15.
f(6)=f(5)-f(4)=-1,
f(7)=f(6)-f(5)=lg3-lg2=f(1),
f(8)=f(7)-f(6)=lg3+lg5=f(2),
∴f(n+6)=f(n),
∴f(2009)=f(5+334×6)═f(5)=-lg15.
故答案为:-lg15.
∴f(3)=f(2)-f(1)=lg5+lg2=1,
∴f(4)=f(3)-f(2)=lg2-lg3,
f(5)=f(4)-f(3)=-lg15.
f(6)=f(5)-f(4)=-1,
f(7)=f(6)-f(5)=lg3-lg2=f(1),
f(8)=f(7)-f(6)=lg3+lg5=f(2),
∴f(n+6)=f(n),
∴f(2009)=f(5+334×6)═f(5)=-lg15.
故答案为:-lg15.
点评:本题考查了利用抽象函数的周期性求函数值,考查了推理能力与计算能力,属于难题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
已知cosα=-
,且π<α<
,则tanα=( )
| 5 |
| 13 |
| 3π |
| 2 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
若α=-835°,则角α的终边在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
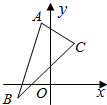 已知△ABC三个顶点是A(-1,4),B(-2,-1),C(2,3).
已知△ABC三个顶点是A(-1,4),B(-2,-1),C(2,3).