题目内容
已知数列{an}的前n项和Sn=2n+2-4 (n∈N*),函数f(x)对?x∈R有f(x)+f(1-x)=1,数列{bn}满足bn=f(0)+f(
)+f(
)+…+f(
)+f(1).
(1)分别求数列{an}、{bn}的通项公式;
(2)若数列{cn}满足cn=an•bn,Tn是数列{cn}的前n项和,若存在正实数k,使不等式k(n2-9n+36)Tn>6n2an对于一切的n∈N*恒成立,求k的取值范围.
| 1 |
| n |
| 2 |
| n |
| n-1 |
| n |
(1)分别求数列{an}、{bn}的通项公式;
(2)若数列{cn}满足cn=an•bn,Tn是数列{cn}的前n项和,若存在正实数k,使不等式k(n2-9n+36)Tn>6n2an对于一切的n∈N*恒成立,求k的取值范围.
考点:数列与不等式的综合,数列的函数特性,数列的求和
专题:等差数列与等比数列
分析:(1)由已知条件利用an=
能求出 an=2n+1 (n∈N*);由f(x)+f(1-x)=1,知f(
)+f(
)=1,由此利用倒序相加法能求出{bn}的通项公式.
(2)cn=an•bn=(n+1)•2n,由此利用错位相减法能求出Tn=n•2n+1.由此得到k>
对于一切的n∈N*恒成立,从而能求出k的取值范围.
|
| 1 |
| n |
| n-1 |
| n |
(2)cn=an•bn=(n+1)•2n,由此利用错位相减法能求出Tn=n•2n+1.由此得到k>
| 6n |
| n2-9n+36 |
解答:
解:(1)∵Sn=2n+2-4 (n∈N*),
∴n=1, a1=S1=21+2-4=4…(1分)
n≥2, an=Sn-Sn-1=(2n+2-4)-(2n+1-4)=2n+1,
n=1时满足上式,
∴ an=2n+1 (n∈N*)…(3分)
∵f(x)+f(1-x)=1,
∴f(
)+f(
)=1,…(4分)
∵bn=f(0)+f(
)+f(
)+…+f(1)①
∴bn=f(1)+f(
)+f(
)+…+f(1)+f(0)②
∴①+②,得2bn=n+1 ∴bn=
.…(6分)
(2)∵cn=an•bn=2n+1•
=(n+1)•2n,
∴Tn=2•2+3•22+4•23+…+n•2n+(n+1)•2n+1,①
2Tn=2•22+3•23+4•24+…+(n+1)•2n+1,②
①-②,得-Tn=4+22+23+…+2n-(n+1)•2n+1
=4+
-(n+1)×2n+1
=-n•2n+1.
∴Tn=n•2n+1.
∵存在正实数k,使不等式k(n2-9n+36)Tn>6n2an对于一切的n∈N*恒成立,
∴k(n2-9n+36)Tn>6n2an恒成立,
∴k>
对于一切的n∈N*恒成立,
∴k>
,
令g(n)=
,则g(n)=
≤
=2.
当且仅当n=6时等号成立,∴g(n)max=2,
∴k>2,即k的取值范围是(2,+∞).
∴n=1, a1=S1=21+2-4=4…(1分)
n≥2, an=Sn-Sn-1=(2n+2-4)-(2n+1-4)=2n+1,
n=1时满足上式,
∴ an=2n+1 (n∈N*)…(3分)
∵f(x)+f(1-x)=1,
∴f(
| 1 |
| n |
| n-1 |
| n |
∵bn=f(0)+f(
| 1 |
| n |
| 2 |
| n |
∴bn=f(1)+f(
| n-1 |
| n |
| n-2 |
| n |
∴①+②,得2bn=n+1 ∴bn=
| n+1 |
| 2 |
(2)∵cn=an•bn=2n+1•
| n+1 |
| 2 |
∴Tn=2•2+3•22+4•23+…+n•2n+(n+1)•2n+1,①
2Tn=2•22+3•23+4•24+…+(n+1)•2n+1,②
①-②,得-Tn=4+22+23+…+2n-(n+1)•2n+1
=4+
| 4(1-2n-1) |
| 1-2 |
=-n•2n+1.
∴Tn=n•2n+1.
∵存在正实数k,使不等式k(n2-9n+36)Tn>6n2an对于一切的n∈N*恒成立,
∴k(n2-9n+36)Tn>6n2an恒成立,
∴k>
| 6n |
| n2-9n+36 |
∴k>
| 6 | ||
n+
|
令g(n)=
| 6 | ||
n+
|
| 6 | ||
n+
|
| 6 | ||
2
|
当且仅当n=6时等号成立,∴g(n)max=2,
∴k>2,即k的取值范围是(2,+∞).
点评:本题考查数列的通项公式 的求法,考查实数的取值范围的求法,解题时要认真审题,注意错位相减法的合理运用.

练习册系列答案
相关题目
已知双曲线
-
=1(a>0,b>0)左,右焦点分别为F1、F2.若在双曲线右支上存在一点P使|PF1|=4|PF2|,则双曲线离心率e的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、(1,
| ||
| B、(1,2] | ||
C、[
| ||
D、[
|
已知空间四边形OABC各边及对角线长都相等,E,F分别为AB,OC的中点,则异面直线OE与BF所成角的余弦值为( )
A、
| ||
B、-
| ||
C、
| ||
D、-
|
在△ABC中,AC=
,BC=2,B=60°,则AB等于( )
| 7 |
| A、4 | B、3 | C、2 | D、1 |
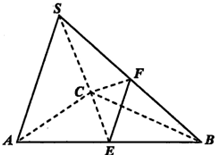 在三棱锥S-ABC中,△ABC是边长为2的正三角形,平面SAC⊥平面ABC,
在三棱锥S-ABC中,△ABC是边长为2的正三角形,平面SAC⊥平面ABC,