题目内容
方程4x2-y2+6x-3y=0表示的图形是 .
考点:二元二次方程表示圆的条件
专题:圆锥曲线的定义、性质与方程
分析:把方程化为圆的标准形式,发现圆的半径等于0,故方程表示一个点.
解答:
解:方程4x2-y2+6x-3y=0 即 4(x+
)2-(y+
)2=0,即4(x+
)2=(y+
)2
∴2x+
=±(y+
),可得:2x-y=0或2x+y+3=0,∴方程表示两条直线.
故答案为:两条相交直线.
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
∴2x+
| 3 |
| 2 |
| 3 |
| 2 |
故答案为:两条相交直线.
点评:本题考查二元二次方程表示圆的条件,二元二次方程x2+y2+dx+ey+f=0 表示圆的充要条件是d2+e2-4f>0.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
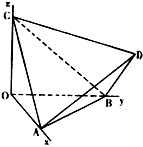 如图,正四面体ABCD的顶点A,B,C分别在两两垂直的三条射线Ox,Oy,Oz上,则在下列命题中,错误的为( )
如图,正四面体ABCD的顶点A,B,C分别在两两垂直的三条射线Ox,Oy,Oz上,则在下列命题中,错误的为( )| A、O-ABC是正三棱锥 |
| B、直线AD与OB所成的角是45° |
| C、直线OB∥平面ACD |
| D、二面角D-OB-A为45° |

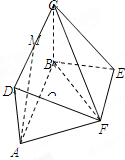 如图,矩形ABCD所在的平面与四边形ABEF所在的平面互相垂直,已知四边形ABEF为等腰梯形,点O为AB的中点,M为CD的中点,AB∥EF,AB=2,AF=EF=1.
如图,矩形ABCD所在的平面与四边形ABEF所在的平面互相垂直,已知四边形ABEF为等腰梯形,点O为AB的中点,M为CD的中点,AB∥EF,AB=2,AF=EF=1. 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,且∠DAB=60°.侧面PAD为正三角形,其所在的平面垂直于底面ABCD,G为AD边的中点.
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,且∠DAB=60°.侧面PAD为正三角形,其所在的平面垂直于底面ABCD,G为AD边的中点.