题目内容
某几何体的三视图如图所示，则该几何体的体积是 ，表面积是 ．
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：由三视图可得该几何体为如图所示：利用长方体与三棱柱的体积与表面积计算公式即可得出．
解答：
解：由三视图可得该几何体为如图所示：
则该几何体的体积V=4×6×3+
×4×3×3=90．
表面积S=2（4×6+4×3+6×3）-3×3+
×4×3×2+
×3+3×4=138．
故答案分别为：90，138．
则该几何体的体积V=4×6×3+
| 1 |
| 2 |
表面积S=2（4×6+4×3+6×3）-3×3+
| 1 |
| 2 |
| 32+42 |
故答案分别为：90，138．
点评：本题考查了长方体与三棱柱的体积与表面积计算公式，属于基础题．
练习册系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
有下列函数①y=x+
（x＞0）；②y=x+
+1（x＞1）；③y=cosx+
（θ＜x＜
）；④y=lnx+
（x＞0），其中最小值为4的函数有（ ）
| 4 |
| x |
| 1 |
| x-1 |
| 1 |
| cosx |
| π |
| 2 |
| 4 |
| lnx |
| A、4个 | B、3个 | C、2个 | D、1个 |
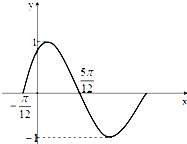函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，φ＜