题目内容
设a,b是两条不同的直线,α、β是两个不同的平面,给出下列四个命题:
①如果a∥α,b∥α,那么a∥b;
②如果a∥β,a?α,b?β,那么a∥b;
③如果 α⊥β,a?α,那么 a⊥β;
④如果a⊥β,a∥b,b?α,那么α⊥β
其中正确命题的序号是( )
①如果a∥α,b∥α,那么a∥b;
②如果a∥β,a?α,b?β,那么a∥b;
③如果 α⊥β,a?α,那么 a⊥β;
④如果a⊥β,a∥b,b?α,那么α⊥β
其中正确命题的序号是( )
| A、① | B、② | C、③ | D、④ |
考点:空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:利用空间中线线、线面、面面间的位置关系求解.
解答:
解:①如果a∥α,b∥α,那么a与b相交、平行或异面,故①错误;
②如果a∥β,a?α,b?β,那么a与b平行或异面,故②错误;
③如果α⊥β,a?α,那么a与β相交、平行或a?β,故③错误;
④如果a⊥β,a∥b,b?α,那么由平面与平面垂直的判定定理得α⊥β,故④正确.
故选:D.
②如果a∥β,a?α,b?β,那么a与b平行或异面,故②错误;
③如果α⊥β,a?α,那么a与β相交、平行或a?β,故③错误;
④如果a⊥β,a∥b,b?α,那么由平面与平面垂直的判定定理得α⊥β,故④正确.
故选:D.
点评:本题考查命题真假的判断,是基础题,解题时要注意空间思维能力的培养.

练习册系列答案
相关题目
若a,b,c依次表示方程2x+x=1,log2x+x=1,log2x+x=2的根,则a,b,c的大小顺序为( )
| A、c<a<b |
| B、a<b<c |
| C、a<c<b |
| D、c<b<a |
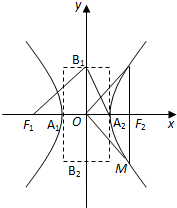 我们把离心率为e=
我们把离心率为e=
| ||
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
①双曲线x2-
| 2y2 | ||
|
②若b2=ac,则该双曲线是黄金双曲线;
③若∠F1B1A2=90°,则该双曲线是黄金双曲线;
④若∠MON=90°,则该双曲线是黄金双曲线.
| A、①② | B、①③ |
| C、①③④ | D、①②③④ |
执行如图所示的程序框图,则输出n的值是( )


| A、8 | B、9 | C、10 | D、11 |
执行如图所示的程序框图,如果输入a=2,b=2,那么输出的a值为( )


| A、14 | B、15 | C、16 | D、17 |
已知过两点A(-1,1),B(4,a)的直线斜率为1,那么a的值是( )
| A、-6 | B、-4 | C、4 | D、6 |
已知集合M={-1,0,1},N={-1,0},则M∩N=( )
| A、{-1,0,1} |
| B、{-1,0} |
| C、{-1,1} |
| D、{1,0} |