题目内容

正六棱柱ABCDEF-A1B1C1D1E1F1的较长的对角线的长为
3
，较短的对角线与底面ABCDEF所成的角为30°，求棱柱的体积．
考点：棱柱、棱锥、棱台的体积
专题：计算题,空间位置关系与距离
分析：设正六棱柱的高为h，底面的边长为a，利用条件，建立方程，求出a，h，即可求出棱柱的体积．
解答： 解：设正六棱柱的高为h，底面的边长为a．
则（2a）2+h2=（
3
）2 …（1）
h
a
=tan30°=
3
3
 …（2）
由（2）式得h=
3
3
a，代入（1）式得a=
3
13

故h=
1
39
　　
而底面积=6×
3
4
×(
3
13
)2=
27
3
26
　　
所以正六棱柱的体积=底面积×高=
27
3
26
×
1
39
=
27
13
338
．
点评：本题考查正六棱柱的体积，考查学生的计算能力，求出正六棱柱的高，底面的边长是关键．
练习册系列答案
相关题目
在△ABC中，角A，B，C的对边分别是a，b，c，且a＞c．已知
BA
•
BC
=2，cosB=
1
3
，b=3．
（1）求a和c的值；
（2）求cosC的值．
已知函数f（x）=
x+a
x+b
（a、b为常数）
（1）若b=1，解不等式f（x-1）＜0；
（2）若a=1，当x∈[-1，2]时，f（x）＞
-1
(x+b)2
恒成立，求b的取值范围．
已知P为椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）上的任意一点，F1，F2为其焦点，则以PF1为直径的圆与圆x2+y2=a2的位置关系为（　　）
A、相交B、内切C、内含D、不确定
如图，在三棱锥A-BCD中，BC=AC，AD=BD，作BE⊥CD，E为垂足，作AH⊥BE于H．求证：AH⊥平面BCD．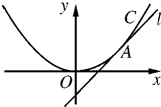
如图，直线l：y=x+b与抛物线C：x2=4y相切于点A．
（1）求实数b的值；
（2）已知圆P经过A点且始终与抛物线C的准线相切，求圆P的圆心的轨迹方程，并说明其是什么曲线？．
∫
1
0
1-x2
dx-
∫
π
0
sinxdx=
 
．
已知双曲线的中心在原点，焦点F1，F2在坐标轴上，离心率为
2
，且过点（4，-2
2
）．
（1）求双曲线方程；
（2）若M是双曲线右支上的点，且
MF1
•
MF2
=0，求△F1MF2的面积．
在△ABC中，已知M是BC中点，设
CB
=
a
，
CA
=
b
，则
AM
=（　　）
A、
1
2
a
-
b
B、
1
2
a
+
b
C、
a
-
1
2
b
D、
a
+
1
2
b

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网