题目内容

∫
1
0
1-x2
dx-
∫
π
0
sinxdx=
 
．
考点：定积分
专题：导数的综合应用
分析：由定积分的几何意义求得
∫
1
0
1-x2
dx，直接求定积分得到
∫
π
0
sinxdx，则答案可求．
解答： 解：求
∫
1
0
1-x2
dx-
∫
π
0
sinxdx．
由定积分的几何意义可知，
∫
1
0
1-x2
dx是以原点为圆心，以1为半径的四分之一圆的面积，等于
π
4
．
∫
π
0
sinxdx=(-cosx)
|
π
0
=-cosπ+cos0=2．
∴
∫
1
0
1-x2
dx-
∫
π
0
sinxdx=
π
4
-2．
故答案为：
π
4
-2．
点评：本题考查了定积分，考查了定积分的几何意义，是基础的计算题．
练习册系列答案
相关题目
下列选项中，可作为函数y=f（x）的图象的是（　　）
A、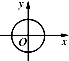
B、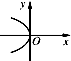
C、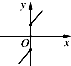
D、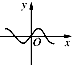
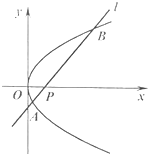已知函数y=f（x）的定义域为[a，b]，a＜c＜b，当x∈[a，c]时，f（x）是单调减函数，当x∈[c，b]时，f（x）是单调增函数，则下列说法正确的是
 
．
①f（x）的最大值为f（c）；
②f（x）的最小值为f（c）；
③f（x）有最小值但无最大值；
④f（x）既有最大值又有最小值；
⑤f（x）的最大值为f（a）．
正六棱柱ABCDEF-A1B1C1D1E1F1的较长的对角线的长为
3
，较短的对角线与底面ABCDEF所成的角为30°，求棱柱的体积．
如图，已知抛物线y2=4x，点P（a，0）是x轴上的一点，经过点P且斜率为1的直线l与抛物线相交于A，B两点．
（1）当点P在x轴上时，求线段AB的中点轨迹方程；
（2）若|AB|=4|OP|（O为坐标原点），求a的值．
定义m*n=
mn-1
-km-2，则方程x*x=0有唯一解时，实数k的取值范围是
 
．
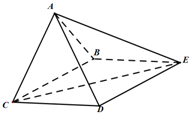四棱锥A-ABCD中，底面BCDE为矩形，侧面ABC⊥底面BCDE，BC=2，CD=
2
，AB=AC．
（Ⅰ）证明：AD⊥CE；
（Ⅱ）若设AC=2，求二面角C-AD-E余弦值．
设椭圆E的中心在坐标原点O，焦点在x轴上，离心率为
3
3
，过点C（-1，0）的直线交椭圆E于A，B两点，且
CA
=2
BC
，求当△AOB面积达到最大时的直线和椭圆的方程．
求不等式
ax
x-3
＞1（a∈R）的解集．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网