题目内容
12.已知等差数列{an}的前n项和Sn满足 S3=0,S5=-5,(1)求数列{an}的通项an;
(2)令${b_n}=\frac{1}{{{a_{2n-1}}•{a_{2n+1}}}}(n∈{N^*})$,求数列{bn}的前n 项和Tn.
分析 (1)方法一:等差数列的前n项和公式可知:$\left\{\begin{array}{l}{3{a}_{1}+\frac{3×2}{2}=0}\\{5{a}_{1}+\frac{5×4}{2}=-5}\end{array}\right.$,即可求得a1和d,根据等差数列的通项公式即可求得数列{an}的通项an;
方法二:根据等差数列前n项和的性质可知:S3=3a2=0,S5=5a3=-5,则d=a3-a2=-1,则an=a2+(n-2)d;
(2)由(1)可知bn=$\frac{1}{2}$($\frac{1}{2n-3}$-$\frac{1}{2n-1}$),采用“裂项法”即可求得Tn.
解答 解:(1)方法一:设等差数列{an}公差为d,
由等差数列的前n项和公式可知:$\left\{\begin{array}{l}{3{a}_{1}+\frac{3×2}{2}=0}\\{5{a}_{1}+\frac{5×4}{2}=-5}\end{array}\right.$,
即$\left\{\begin{array}{l}{{a}_{1}+d=0}\\{{a}_{1}+2d=-1}\end{array}\right.$,解得a1=1,d=-1,
则{an}的通项公式an=1-(n-1)=2-n;
方法二:由等差数列前n项和的性质可知:S3=3a2=0,则a2=0,
S5=5a3=-5,则a3=-1,
d=a3-a2=-1,
∴数列{an}的通项公式an=a2+(n-2)d=2-n;
(2)由(1)可知:bn=$\frac{1}{{a}_{2n-1}•{a}_{2n+1}}$=$\frac{1}{(3-2n)(1-2n)}$=$\frac{1}{(2n-1)(2n-3)}$=$\frac{1}{2}$($\frac{1}{2n-3}$-$\frac{1}{2n-1}$),
数列{bn}的前n 项和Tn=$\frac{1}{2}$(-1-1)+$\frac{1}{2}$(1-$\frac{1}{3}$)+$\frac{1}{2}$($\frac{1}{3}$-$\frac{1}{5}$)+…+$\frac{1}{2}$($\frac{1}{2n-3}$-$\frac{1}{2n-1}$),.
=$\frac{1}{2}$(-1-1+1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+…+$\frac{1}{2n-3}$-$\frac{1}{2n-1}$),
=$\frac{1}{2}$(-1-$\frac{1}{2n-1}$),
=$\frac{n}{1-2n}$,
数列{bn}的前n 项和Tn=$\frac{n}{1-2n}$.
点评 本题考查等差数列的性质及前n项和公式,考查“裂项法”求数列的前n项和,考查计算能力,属于中档题.

| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
| A. |  | B. |  | C. |  | D. |  |
| 年份 | 2011 | 2012 | 2013 | 2014 | 2015 |
| 年份代号t | 1 | 2 | 3 | 4 | 5 |
| 人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 |
(2)利用(1)中的回归方程,分析2011年至2015年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2016年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:$\left\{{\begin{array}{l}{\hat b=\frac{{\sum_{i=1}^n{({{x_i}-\overline x})({{y_i}-\overline y})}}}{{\sum_{i=1}^n{{{({{x_i}-\overline x})}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x}•\overline y}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}}\\{\hat a=\overline y-\hat b\overline x}\end{array}}\right.$.
| A. | $\frac{2π}{3}$ | B. | $\frac{π}{2}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
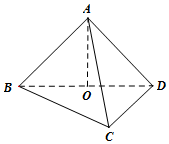 (文科)设A在平面BCD内的射影是直角三角形BCD的斜边BD的中点O,
(文科)设A在平面BCD内的射影是直角三角形BCD的斜边BD的中点O,