题目内容
若直线l1：ax+2y+6=0与直线l2：x+（a-1）y+6=0平行，则实数a=（ ）
A、
| ||
| B、2 | ||
| C、-1 | ||
| D、-1或2 |
考点：直线的一般式方程与直线的平行关系
专题：直线与圆
分析：两直线的斜率都存在，由l1与l2平行得：
=
，解出a的值．
| a |
| 2 |
| 1 |
| a-1 |
解答：
解：由题意知，两直线的斜率都存在，由l1与l2平行得
=
，∴a=-1 a=2，
故选：D．
| a |
| 2 |
| 1 |
| a-1 |
故选：D．
点评：本题主要考查两直线平行的性质，两直线平行，斜率相等，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图所示，向量曲线y=3x-x3上切点为p（2，-2）的切线方程是（ ）
| A、y=-9x+16 |
| B、y=9x-20 |
| C、y=-2 |
| D、y=-9x+16或y=-2 |
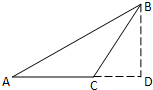已知△ABC为等腰三角形，∠A=∠B=30°，BD为AC边上的高，若| AB |
| a |
| AC |
| b |
| BD |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
已知函数f(x)=
的定义域为R，则（ ）
| cos(sinx) |
| A、f（x）是奇函数 |
| B、f（x）是偶函数 |
| C、f（x）即是奇函数又是偶函数 |
| D、f（x）即不是奇函数又不是偶函数 |
已知奇函数f（x）在区间[-2，2]上单调递减，则不等式f（x2）+f（2x）＞0的解集是（ ）
| A、[-1，0） |
| B、（-2，0） |
| C、（-2，-1] |
| D、（-∞，-2）∪（0，+∞） |