题目内容
设p:函数f(x)=
的定义域为R;q:不等式ax>1的解集是{x|x<0},如果命题“p∨q”为真命题,命题“p∧q”为假命题,求实数a的取值范围.
| ax2-x+a |
考点:复合命题的真假
专题:简易逻辑
分析:本题考查的知识点是复合命题的真假判定,解决的办法是先判断组成复合命题的简单命题的真假,再根据真值表进行判断.
解答:
解:∵p:函数f(x)=
的定义域为R
∴若p为真,那么ax2-x+a≥0对于任意的x∈R成立
①当a=0,不成立
②当a>0,△=1-4a2<0,
∴a>
③a<0,那么ax2-x+a≥0对于任意的x∈R不能成立
∴若p为真,那么a>
又∵q:不等式ax>1的解集是{x|x<0}
∴若q为真,那么,0<a<1
∵p且q”为假命题,“p或q”为真命题
∴p、q一真一假
①p真q假,那么a的取值范围:[1,+∞)
②p假q真,那么a的取值范围:(0,
]
综上所述:a∈(0,
]∪[1,+∞)
| ax2-x+a |
∴若p为真,那么ax2-x+a≥0对于任意的x∈R成立
①当a=0,不成立
②当a>0,△=1-4a2<0,
∴a>
| 1 |
| 2 |
③a<0,那么ax2-x+a≥0对于任意的x∈R不能成立
∴若p为真,那么a>
| 1 |
| 2 |
又∵q:不等式ax>1的解集是{x|x<0}
∴若q为真,那么,0<a<1
∵p且q”为假命题,“p或q”为真命题
∴p、q一真一假
①p真q假,那么a的取值范围:[1,+∞)
②p假q真,那么a的取值范围:(0,
| 1 |
| 2 |
综上所述:a∈(0,
| 1 |
| 2 |
点评:本题考查的知识点是复合命题的真假判定,属于基础题目

练习册系列答案
相关题目
若直线l1:ax+2y+6=0与直线l2:x+(a-1)y+6=0平行,则实数a=( )
A、
| ||
| B、2 | ||
| C、-1 | ||
| D、-1或2 |
以初速度40m/s竖直向上抛一物体,t秒时刻的速度v=40-10t2,则此物体达到最高时的高度为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
非零向量
,
使得|
-
|=|
|+|
|成立的一个充分非必要条件是( )
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|
在△ABC中,A=60°,a=4
,b=4
,则B=( )
| 3 |
| 2 |
| A、30° | B、45° |
| C、120° | D、135° |
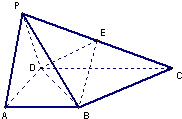 如图,四棱锥P-ABCD的底面ABCD为一直角梯形,侧面PAD是等边三角形,其中BA⊥AD,CD⊥AD,CD=2AD=2AB,平面PAD⊥底面ABCD,E是PC的中点.
如图,四棱锥P-ABCD的底面ABCD为一直角梯形,侧面PAD是等边三角形,其中BA⊥AD,CD⊥AD,CD=2AD=2AB,平面PAD⊥底面ABCD,E是PC的中点.