题目内容
已知函数f（x）=x2-2ax+2，求f（x）在[-1，1]上的最小值．
考点：二次函数在闭区间上的最值
专题：函数的性质及应用
分析：对于函数f（x）=x2-2ax+2=（x-a）2+2-a2，分对称在区间[-1，1]的左侧、中间、右侧三种情况，分别求得f（x）在[-1，1]上的最小值．
解答：
解：函数f（x）=x2-2ax+2=（x-a）2+2-a2，
当a＜-1时，f（x）在[-1，1]上的最小值为f（-1）=2a+3；
当-1≤a≤1时，f（x）在[-1，1]上的最小值为f（a）=2-a2；
当a＞1时，f（x）在[-1，1]上的最小值为f（1）=3-2a．
当a＜-1时，f（x）在[-1，1]上的最小值为f（-1）=2a+3；
当-1≤a≤1时，f（x）在[-1，1]上的最小值为f（a）=2-a2；
当a＞1时，f（x）在[-1，1]上的最小值为f（1）=3-2a．
点评：本题主要考查求二次函数在闭区间上的最值，二次函数的性质的应用，体现了分类讨论的数学思想，属基础题．
练习册系列答案
相关题目
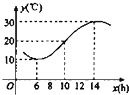某地一填从6时至14时的温度函数变化曲线近似满足y=Asin（ωx+φ）+b（|φ|＜π）
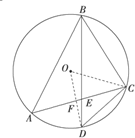如图，⊙O是△ABC的外接圆，D是 