题目内容
求下列函数的解析式
(1)一次函数f(x)满足f[f(x)]=4x+3,求f(x);
(2)已知函数f(x-1)=x2-x+1,求f(x).
(1)一次函数f(x)满足f[f(x)]=4x+3,求f(x);
(2)已知函数f(x-1)=x2-x+1,求f(x).
考点:函数解析式的求解及常用方法
专题:计算题,函数的性质及应用
分析:(1)运用待定系数法求解,转化为恒等问题解决.(2)利用换元法,或整体配送的方法求解即可.
解答:
解:(1)设f(x)=kx+b(k≠0)则f[f(x)]=k(kx+b)+b=k2x+kb+b
∴k2x+kb+b=4x+3
则
解得
或
∴f(x)=2x+1或f(x)=-2x-3
(2)方法一:f(x-1)=x2-x+1=(x-1)2+(x-1)+1
∴f(x)=x2+x+1)
方法二:设t=x-1则x=t+1
则f(t)=(t+1)2-(t+1)+1=t2+t+1
∴f(x)=x2+x+1
∴k2x+kb+b=4x+3
则
|
|
|
∴f(x)=2x+1或f(x)=-2x-3
(2)方法一:f(x-1)=x2-x+1=(x-1)2+(x-1)+1
∴f(x)=x2+x+1)
方法二:设t=x-1则x=t+1
则f(t)=(t+1)2-(t+1)+1=t2+t+1
∴f(x)=x2+x+1
点评:本题考查了函数解析式求解的常见的方法,难度不大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
三个数a,b,c成等比数列,公比q=3,又a,b+8,c成等差数列,则这三个数依次为( )
| A、3,9,27 |
| B、27,9,3 |
| C、36,12,4 |
| D、4,12,36 |
一棱台两底面周长的比为1:5,过侧棱的中点作平行于底面的截面,则该棱台被分成两部分的体积比是( )
| A、1:125 |
| B、27:125 |
| C、13:49 |
| D、13:62 |
 下面四个命题:
下面四个命题: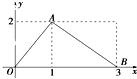 函数f(x)的图象是如下图所示的折线段OAB,点A的坐标为(1,2),点B的坐标为(3,0)
函数f(x)的图象是如下图所示的折线段OAB,点A的坐标为(1,2),点B的坐标为(3,0)